平面図形 それぞれの図形において,図形の性質を以下のように学習しています。(一部抜粋) 2年 4年 3年 6年 5年 中学数学 2年2-3① さらにくわしくお知りになりたい場合 教授用資料 啓林館教師用指導書2年 指導研究編 p56 5 図形の性質と証明 既習内容2年「図形の性質と証明」 チャレンジシート② 基本 A B D C 2 $ ' % & fp fp \fp fp $ ' % ( & \ 次 の図 で ,四角 形$%&'は平行 辺 ある 。こ とき \ 値を求めよ図形の性質図形の証明の考え方 図形の性質平行線の作図(内分点,外分点の作図について) 図形の性質方べきの定理ってどういうときに出てくるんですか? 図形の性質回転体で「内部が通過する部分」と「側面が通過する部分」の意味
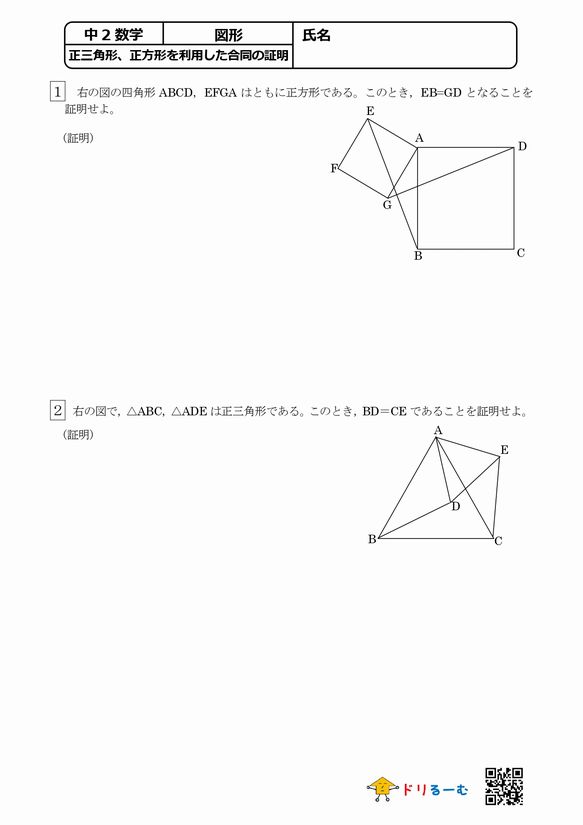
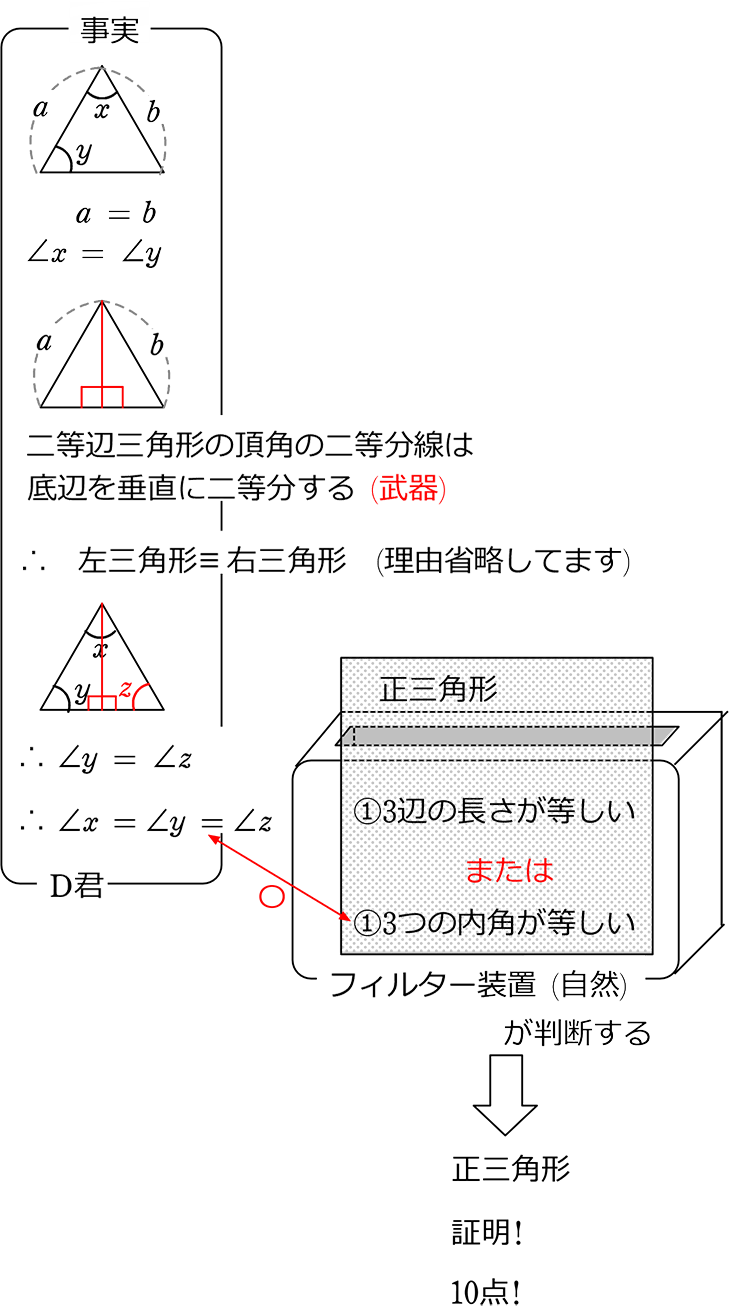
正三角形 正方形を利用した合同の証明 ドリるーむ
図形の性質の証明 中3 円
図形の性質の証明 中3 円-合同の証明 証明とは 仮定や図形の性質を根拠として結論を導く。 等式を用いて説明するが、どの式にも 理由が必要 である。 三角形の合同を証明する 三角形の合同条件をそろえることで証明できる 例1 cはadの中点で, ∠bac=∠edcのとき bac≡ edcとなること合同な図形は相似な図形でもあるので、この2つの図形は相似となる。 相似比 相似な図形で、対応する線分の長さの比を相似比(そうじひ)といいます。 三角形の相似条件 2年生では三角形が合同になる条件を考えました。



S Aℓの証明 式の計算の利用 図形編 教遊者
図形 定義・定理 まとめ 対頂角 𝟖は等しい 直線の角度 ° 平行線の 同位角 𝟖 は等しい 角形の内角の和 °×(𝒏− ) 平行線の 多角形の外角の和錯角 𝟔は等しい ° 同位角 が等しければ、2直線は平行 〇 合同な図形の対応する線分や角は等し2年 5章 図形の性質と証明 ⑥の解答 ( )組( )番 名前( ) Title 2年5章図形の性質と証明①の解答 Author tosyo01 Created Date AM「不思議な公式の証明!」 ~性質が成り立つ理由を式を使って説明する~ ☆本時のねらい:展開や因数分解を利用して図形の性質を証明することができる。 ☆本時の工夫点:①証明のかき方に慣れるために,教科書の証明を読み取り,理解する 時間を設定
>@ >a >b >c >d (証明) 仮定から、AE//FC ・・・①図形の性質の証明がわからないという生徒 の代表的な声の中には、 ¾ 見た目で判断して何でいけないのか? ¾ 当たり前のことをなぜ証明しなければいけないの か? のように、「証明そのもの難しさ」だけでなく 「証明の意義や必要性」に関わる内容が少なまた,図形の性質を証明する指導についても,演 繹的な推論の進め方について理解させたり,証明 を書く前に推論したことを整理させたりする指 導についても十分に行ってこなかった。 Ⅱ 研究の目的 本研究では,図形領域における数学的に推論す
2年生 5 図形の性質と証明 証明の方針2 証明の方針2の( ① )に当てはまる言葉を書きなさい。また, ② に当てはまるこ とがらを,下のアからオの中から1つ選びなさい。 ア対角線が垂直に交わる イ対角線の長さが等しい ウ対角線が平行である「図形の性質」q&a一覧 図形の性質チェバの定理(三角形の頂点を通る3つの直線が三角形の外部で交わるとき) 図形の性質内分点と平行線の作図の仕方について 図形の性質図形の証明の考え方 図形の性質外分点の作図の仕方2 問題の通りに図形が描けているか確認 3 平行や直角を見つける 31 隠れた平行 32 隠れた直角 4 証明問題を解くコツ4つ 41 1とにかく図形の性質や条件を覚える 42 2「仮定」と「結論」をチェック、仮定を図に書き込む 43 3結論を見て、覚えた図形の




公式一覧と使い方 解き方 数学a 図形の性質 教科書より詳しい高校数学




S Aℓの証明 式の計算の利用 図形編 教遊者
5章 図形の性質と証明 1.プリント ダウンロード レベル 1 証明のポイント ①条件をすべて満たしていることを示す。 ②その根拠も必ず示す。 この二つのポイントがわかっていれば、図形の証明もばっちりです。 合同の証明をしてみよう では実際に合同の証明をしてみましょう。2年生 5 図形の性質と証明 この証明のあと,図1と形の違う図2のような平行四辺形ABCDについても,同じようにAF=C Eとなるかどうかを考えてみたところ,下のアからエのような意見が出ました。正しいものを1つ 選びなさい。



角の二等分線とは 定理や比の性質 証明 問題 作図方法 受験辞典
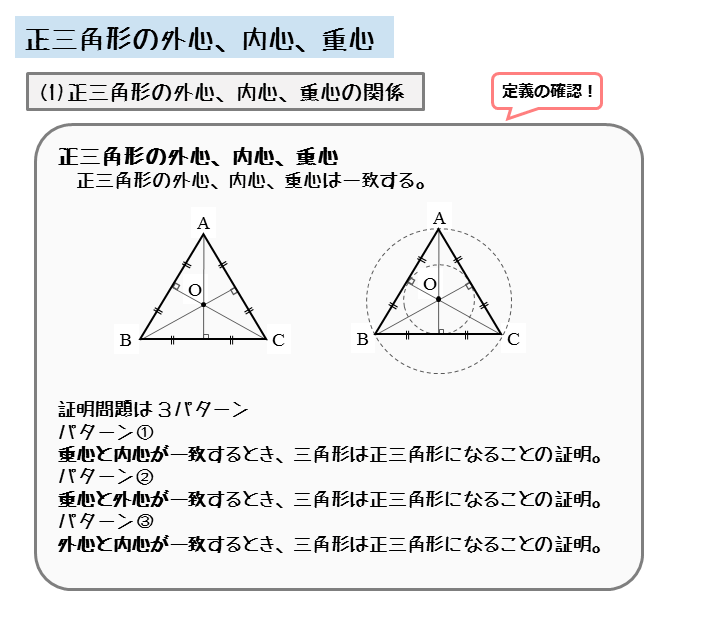



図形の性質 正三角形の外心 内心 重心について 日々是鍛錬 ひびこれたんれん
垂心の性質《証明》 三角形の垂心がもつ性質の証明をします。 まずは「 四角形adhf,behd,cfheは円に内接する四角形である 」を証明していきます。 これには、中学3年生で習った 円周角の定理 を使うと理解が早いです。平行四辺形の証明問題とは、大きく分けて以下の2つだね 平行四辺形の性質を利用した合同の証明 平行四辺形になることを証 図形と証明 直角三角形の合同条件証明問題の書き方とは? イチから徹底解説! kaztastudy 今回は中2で学習する数学25章図形の性質と証明「逆と反例」<基本問題> 組 番 名前 1次のことがらについて,正しいものには ,正しくないものには×をつけ,正しくない場合は反 例を1 つあげなさい。(1)ab>0ならば,a<0,b<0である。 中2・数学5章 図形の性質と証明




これで点が取れる 単元末テスト中2数学 5章 図形の性質と証明




中学数学 合同な図形の性質とは 見つけ方は 問題を使って解説 数スタ
⑤ 証明のしくみ 2 証明の仕組み 図形の性質を証明したり、証明 を読んで新たな性質を見いだす こと 基本の問題 1 本節のまとめと確かめの問題 4章のたしかめ 1 A問題(主に知識・技能の問題) B問題(活用の問題) 8 本時について・証明の方針を基に,証明をまとめるこ 第四次 相似な図形の性質を用い,日常生活の事象 とができるようにする。 や図形の性質などを考える。(3:本時1/3) (2)本時の学習 ①目標 図形の性質について,証明の方針を立てて証明することができる。 ②本時の展開四角形AECFは平行四辺形である。これを証明し なさい。 単 元 年 組 番 7問 2年「図形の性質と証明」 氏名 チャレンジシート③ ジャンプ(解答) PKO PO 斜辺と他の1辺 POH >?



1



Www Shinko Keirin Co Jp Keirinkan Chu Math Support Keyseat Data Sugaku 2nen2 03 Pdf
平行四辺形の定義と性質・証明問題の解き方 管理人 2月 23, 19 中学二年生で習う平面図形の単元ではいろんな図形の性質を利用して問題を解きますが、その中で代表的な図形のひとつが平行四辺形で図形の包摂関係 中学数学 2年3-1② さらにくわしくお知りになりたい場合 教授用資料 啓林館教師用指導書2年 指導研究編 p59~63,107 /啓林館教師用指導書2年 朱註編 p140 5 図形の性質と証明 5章の数学25章図形の性質と証明「三角形の性質」<基本問題①> 組 番 名前 1右の図で,「二等辺三角形の2つの底角は等しい。」という性質を証明す るには,次のア~エのことがらをどのような順序でいえばよいか,もっと も適切なものを記号で答えなさい。



位置ベクトルの内積の利用の証明の例題でbhとacの垂直とかchとab Yahoo 知恵袋



Http Www Saga Ed Jp Kenkyu Kenkyu Chousa H24 04 chu Suugaku Documents Purinto2 5 Ikatsu Shikou Ren Pdf
② 相似な図形の性質を用い て,相似な図形の対応する 辺の長さを求めることがで きる。 ① 図形の相似の意味や相似な 図形の性質を理解している。 ② 三角形の相似条件に関心 をもち,それについて考え たり,それを用いて証明し たりしようとしている。「性質」 :平行四辺形と呼ばれるものには 共通してこんなことが言えるね! 「定理」 :性質の中で特に大切なこと! だから証明はいらないよ! こんな感じです。 例えば、コーラ。 定義:黒くてシュワっとする飲み物図形の性質の証明を読んで新たな性質を見い出したりすること。 数学への 関心・意欲・態度 数学的な見方や考え方 数学的な技能 数量や図形などについ ての知識・理解 様々な事象を平行線の




図形の性質に関する記事一覧




中3数学 式の展開と因数分解 図形の性質の証明 Youtube
証明すべき2つの三角形で共通のこと(一つの辺を共有している場合など) 図形や基本的な幾何の性質 3の「図形や基本的な幾何の性質」ですが、以下のような性質をよく用います。 対頂角:二直線が交わってできる向かい合った角は必ず等しい step4 合同な図形の性質をつかう! 合同な図形の性質をつかってあげよう。 対応する辺の長さはそれぞれ等しいから、 ac = db になるね。 acとdbは長方形abcdの対角線だね?? だから、 長方形の対角線同士が等しいっていえるんだ! 性質③1 本の対角線は、ひし形を合同な 2 つの二等辺三角形に分ける 性質④2 本の対角線は、ひし形を合同な 2 つの直角三角形に分ける;




中2数学 図形の性質と証明 折り目の角を求める Youtube
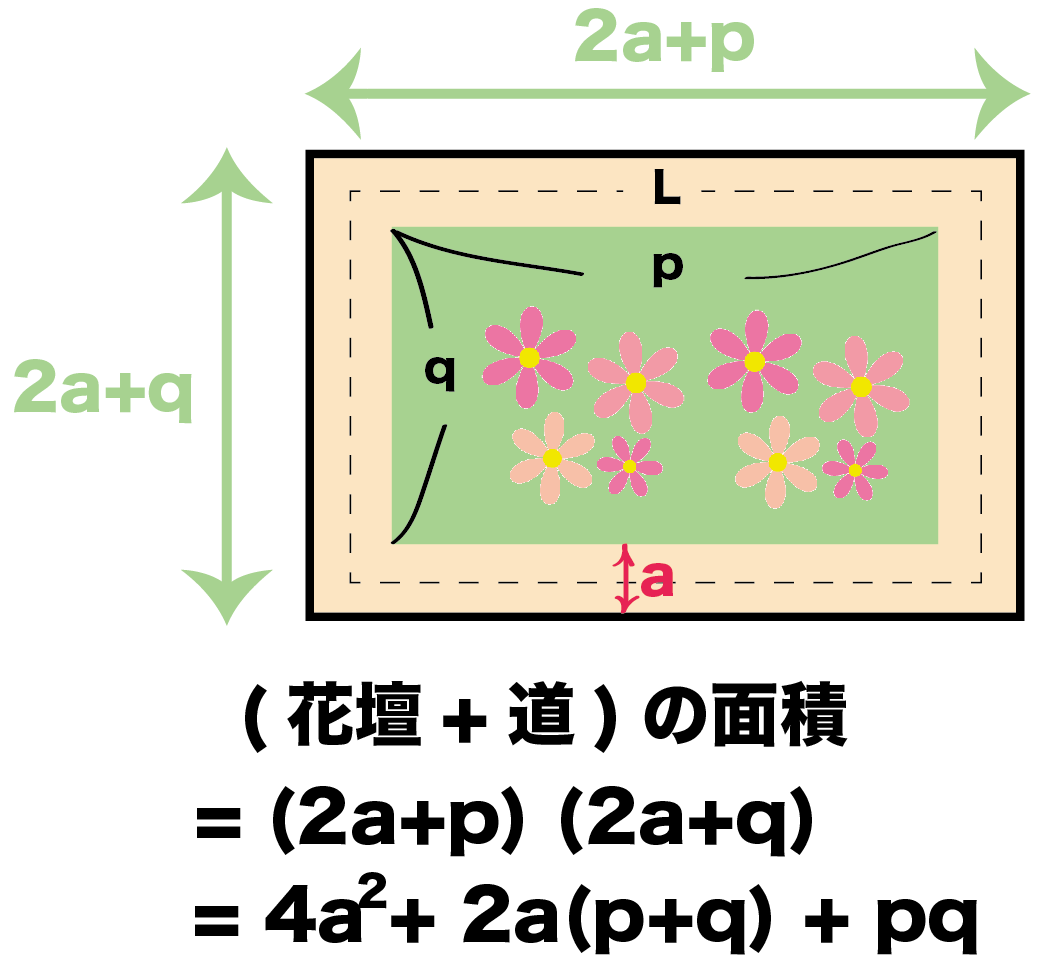



式の計算の利用 図形の証明問題の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく
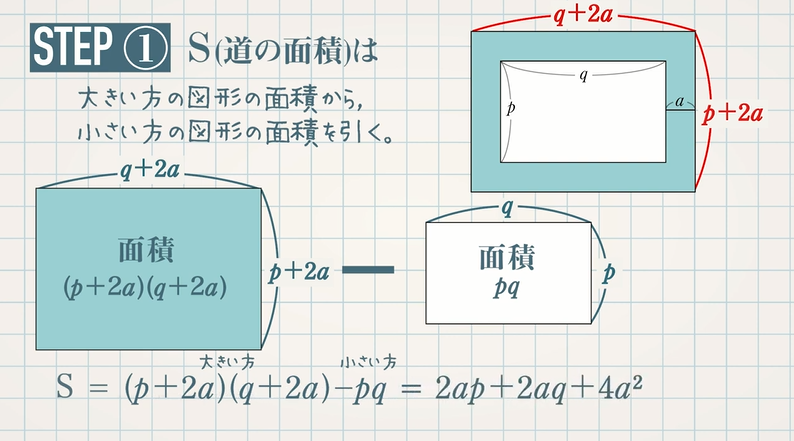
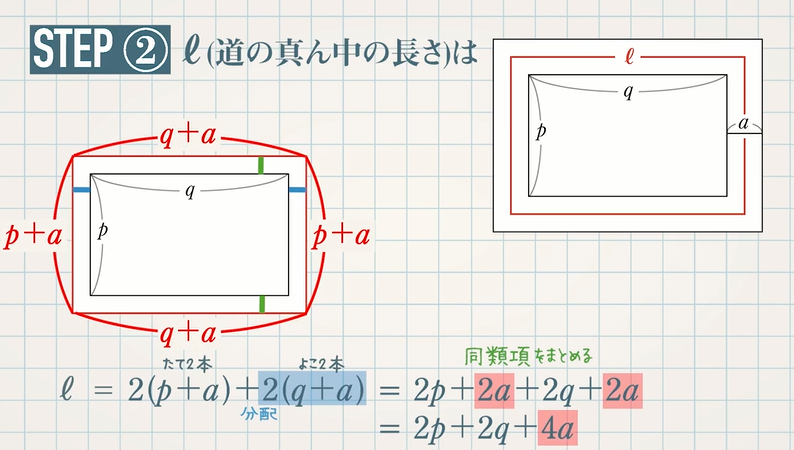
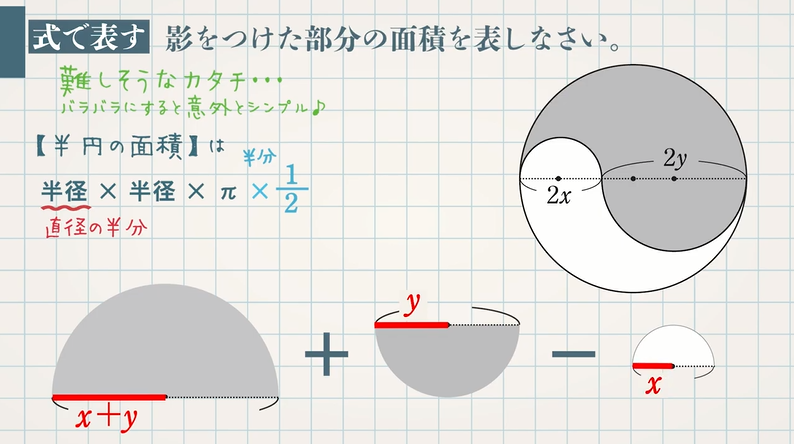
・平行四辺形の性質を利用して、図形の証明をすることができる。 ・証明の結果からわかった、新たな性質を理解することができる。 (2)本時の指導について 本時の授業では、関連づけを図る(別の場面に置き換える)課題を扱い、平行四辺形の性質 これこそが、図形問題なのである。 測ったらタルトが本当に45度で切られていて見事だった 肩慣らしとして、これを解いてみよう。 出題は、「xの角度を求めよ」。 三角形の内角の和は180度。 かつタルトは二等辺三角形なので、角ABCは (180度45度)/2 = 675円の図形による証明 半径 mの円の周囲に,幅 mの道がある。 この道の面積を ㎡,道の真ん中を通る円周の長さを mとするとき, であることを証明しなさい。 まずは、大きな円から小さい円を取り除いて道の面積Sを求めましょう。 今回は円なので、半径
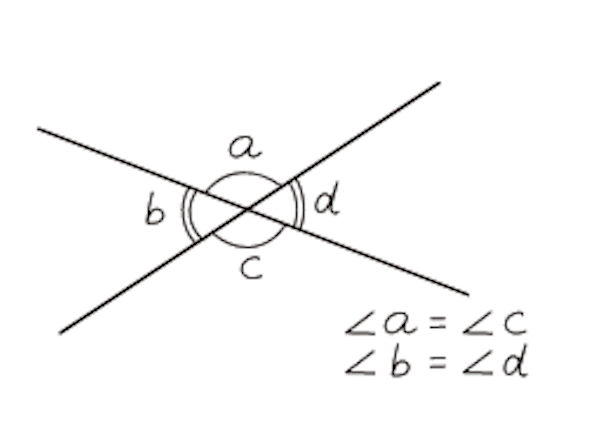



中2数学 図形の調べ方 と 図形の性質と証明 の基礎を解説 札幌市 西区 琴似 発寒 塾 学習塾 個別指導塾 マナビバ
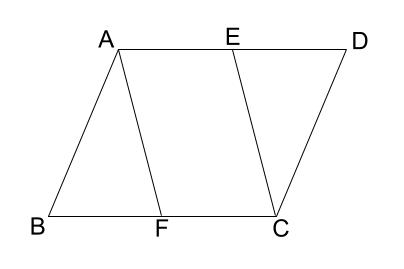



中学数学 証明 平行四辺形の性質の利用 中学数学の無料オンライン学習サイトchu Su
『図形の性質と合同』は具体物だけの操作に終わ ることなく、筋道を立てて説明をすることが求め られている。三角形の角、図形の合同などについ ての基礎的な性質を身に付けさせ、証明の仕組を それらの図形の性質と関連づけて理解させること図形の定義や性質は,もう一度確認しておくこと。 ∠x=180°-(27°+113°)=40° 1 2 2 1 図形の性質,三角形の合同,証明 中学2年 数学 基本問題 4-①




โน ตของ 受験対策 図形の性質 合同 証明 ช น Junior Clear




ม 2 โน ตของ 数学 中2 図形の性質と証明 ช น Junior Clear
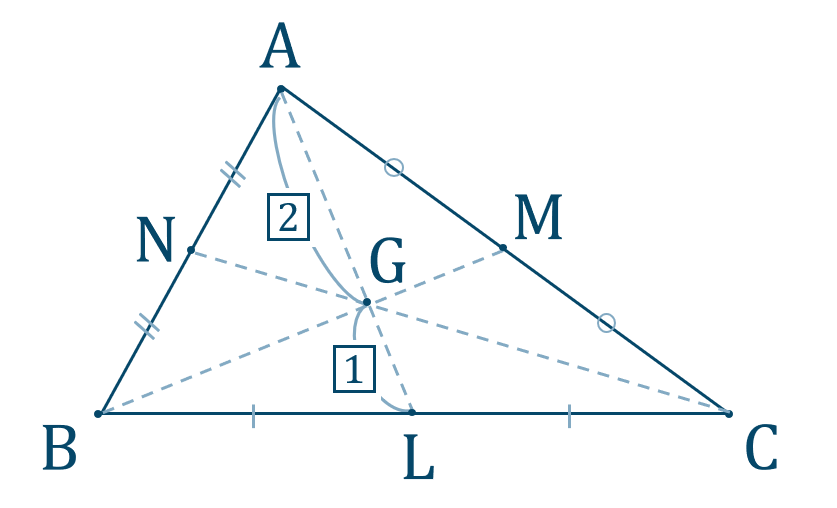



公式一覧と使い方 解き方 数学a 図形の性質 教科書より詳しい高校数学




1 Dabcd Cd M Am A D Descubre Como Resolverlo En Qanda
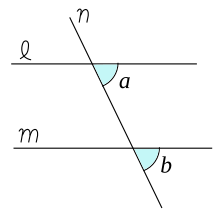



中学校数学 2年生 図形 図形の調べ方 Wikibooks




美しい図形の性質 極線を2回書くと 東大に文理両方で合格した男が綴る 受験の戦略




図形の性質と証明 数スタ
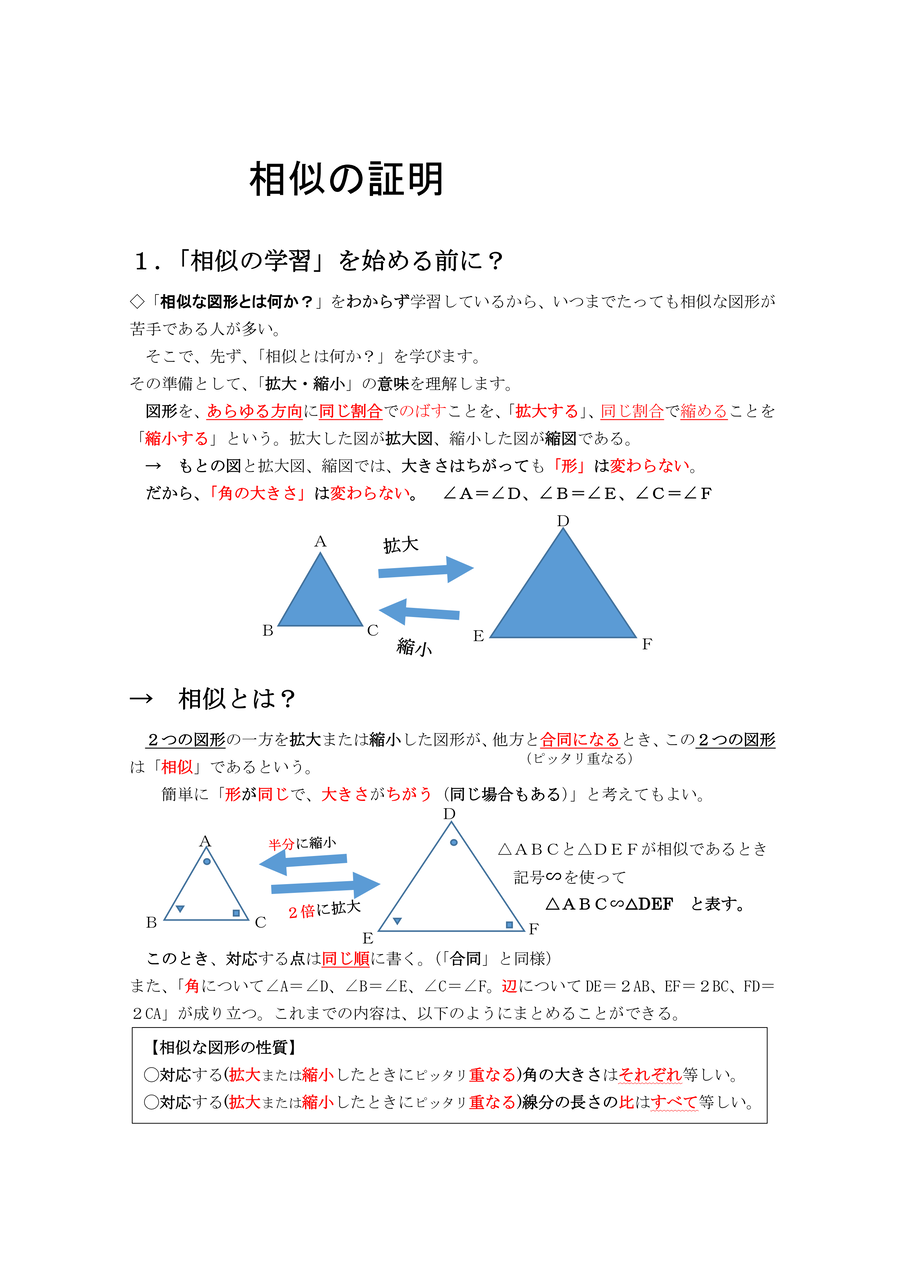



中学校数学 証明のコツ 相似



Www Shinko Keirin Co Jp Keirinkan Chu Math Support Keyseat Data Sugaku 2nen3 01 Pdf



1



図形の性質の証明中3この問題がわからなくて 質問させていただきましたかだんの Yahoo 知恵袋




単元別整理 2年5章 図形の性質と証明 ワカデキな中学校数学




令和3 21 年度用 中学校数学 内容解説資料a




世界一わかりやすい数学問題集中2 5章 図形の性質と証明




苦手な人が多い図形の証明問題を解くコツを解説 実は非常に簡単なんです 学習塾 Step By Step




5章 図形の性質と証明 愛知県公立高校入試 数学 単元別過去問 問題プリントと解答 解説
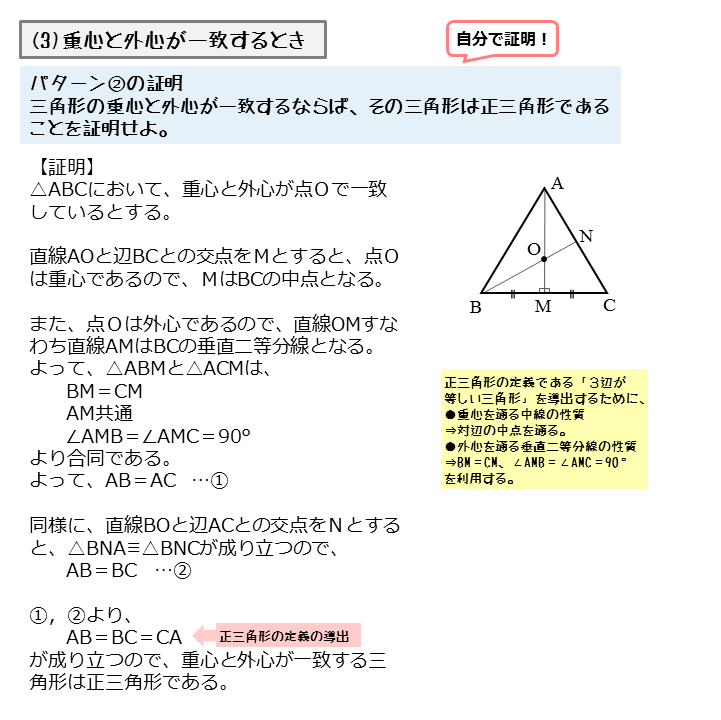



図形の性質 正三角形の外心 内心 重心について 日々是鍛錬 ひびこれたんれん




Thumb M Mathpresso Io Qanda Thumbnail Storage Q
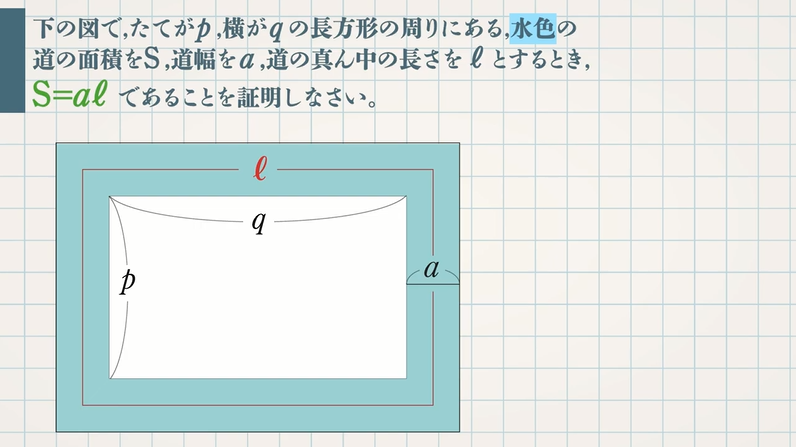



S Aℓの証明 式の計算の利用 図形編 教遊者




中学校数学 2年生 図形 図形の調べ方 Wikibooks
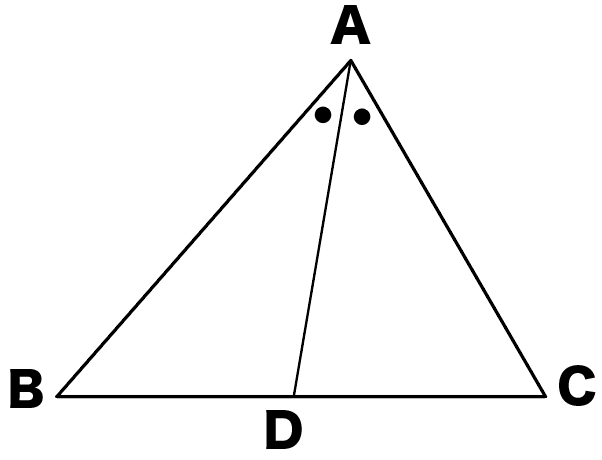



三角形の角の二等分線の性質 定理の証明がわかる5ステップ Qikeru 学びを楽しくわかりやすく




数学 中3 14 式の計算の利用 図の証明編 Youtube




中学2年生 数学 合同と証明 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



中学数学 図形の合同 図形の性質




中2数学 図形の性質と証明 1 2 二等辺三角形 1 Youtube




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学



前ちゃんの中学校数学の部屋 証明の導入または図形の調べ方の課題学習



Www Shimane Fuzoku Ed Jp Wp Wp Content Uploads 17 03 10 C2 Sugaku Pdf




中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット
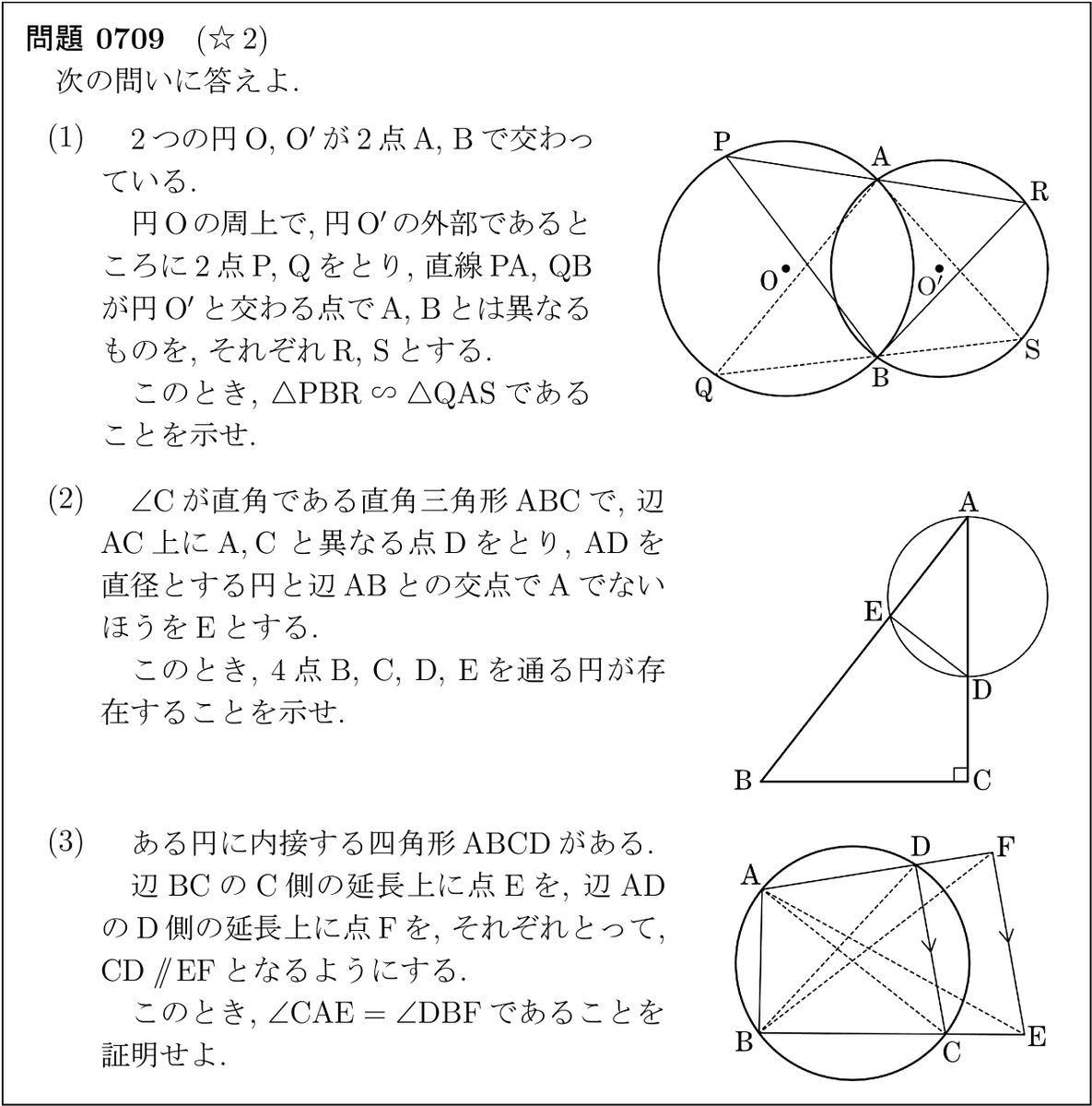



高校数学基本問題垂れ流し Ar Twitter 07 図形の性質 2 円 円周角 円に内接する四角形 4点が同一円周上にある条件と証明
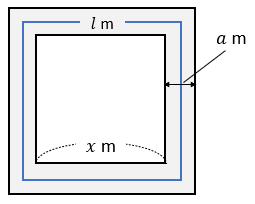



中3 式の計算の利用 円 正方形の図形の証明をイチから 数スタ



角の二等分線の性質と二等分線の長さ 思考力を鍛える数学




2年ー5章ー図形の性質と証明 ワカデキな中学校数学




数学 中2 60 証明のしくみ Youtube



因数分解でやる 図形の証明がわかりません 正方形や長方形はできたのですが 長方 Yahoo 知恵袋
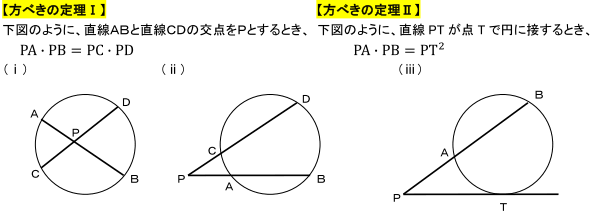



方べきの定理ってどういうときに出てくるんですか 数学 苦手解決q A 進研ゼミ高校講座



S Aℓの証明 式の計算の利用 図形編 教遊者




三角形の重心の性質とその証明 求め方 数学a By となりがトトロ マナペディア



図形の性質 式の利用 その他 教遊者




中学生 図形の性質と証明のノート一覧 Clear



中2数学 図形の証明問題では様々な図形の性質を理解することが大切 中学生 受験対応 英語 数学 学習講座




中3数学 円の性質17 円の性質を利用した証明 すべて無料 星組の中学数学講座




図形に関する性質の証明 身勝手な主張




中2 中2 数学 5章 図形の性質と証明 プレイカラー 中学生 数学のノート Clear
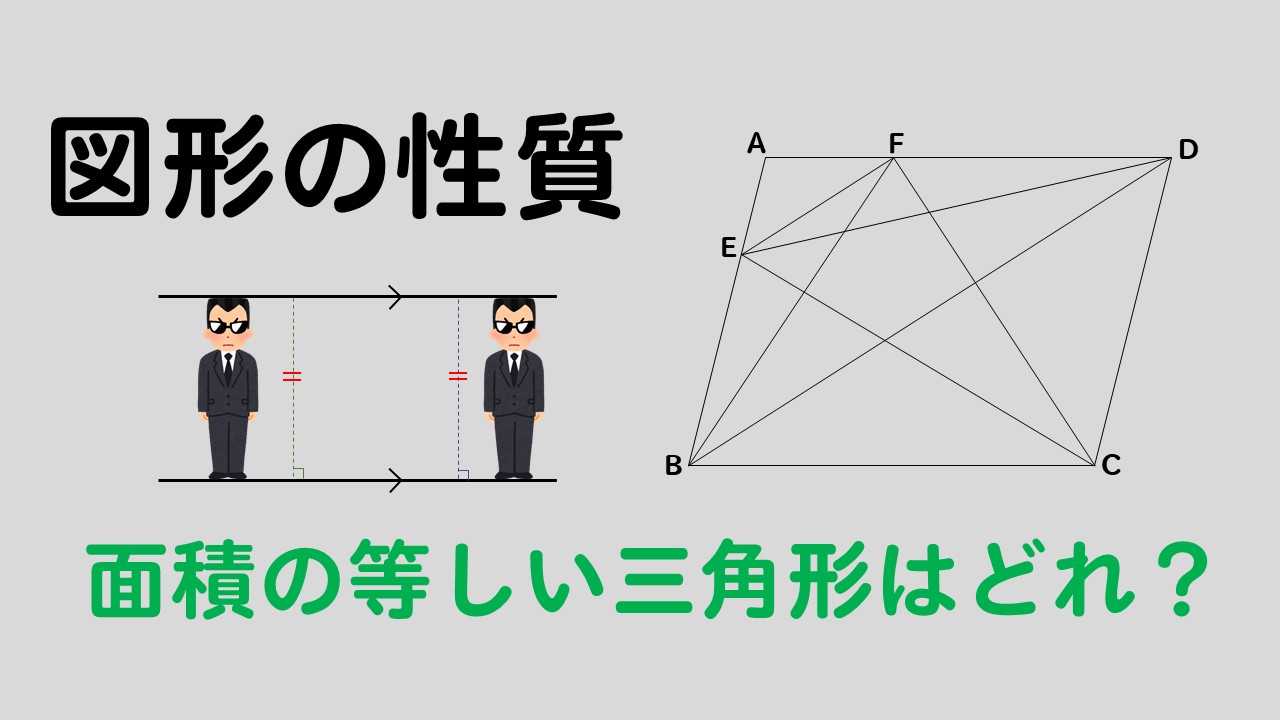



中2数学 平行四辺形の中から面積の等しい三角形を見つける問題を解説 数スタ
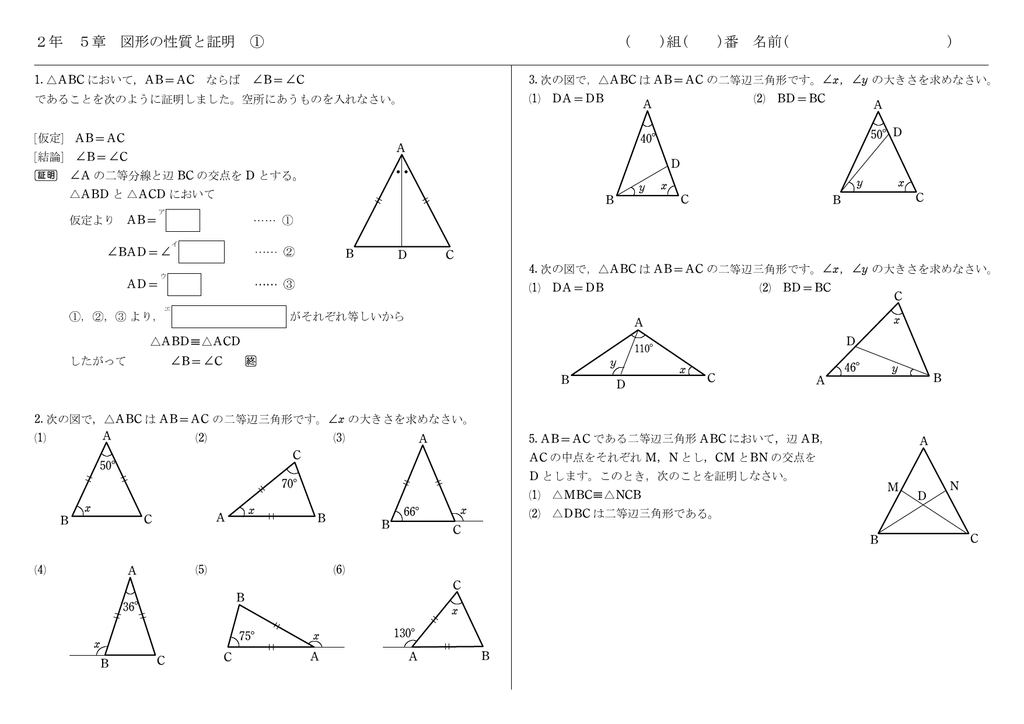



2年 5章 図形の性質と証明




世界一わかりやすい数学問題集中2 5章 図形の性質と証明




図形の性質の調べ方 最新版 中学生 数学のノート Clear



中3第1章5 式の計算の利用6 図形の性質の証明 写真日記



1




S A R Descubre Como Resolverlo En Qanda
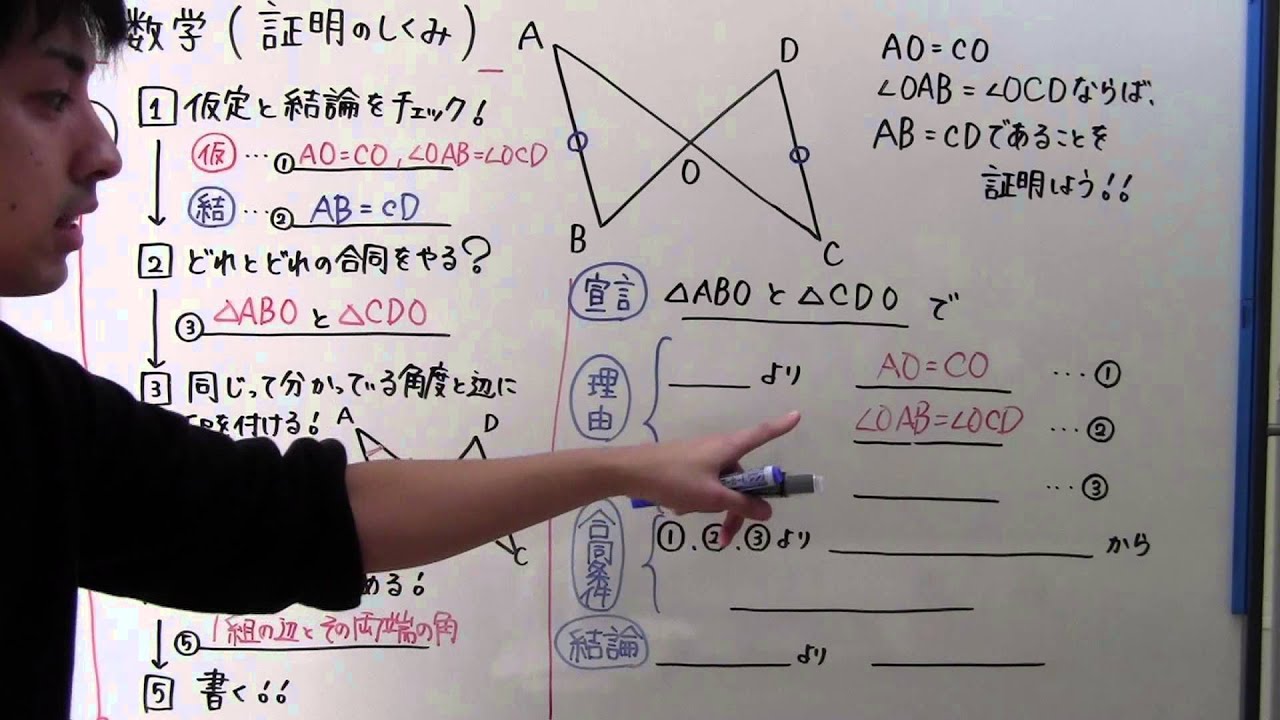



中2 数学 中2 60 証明のしくみ Youtube
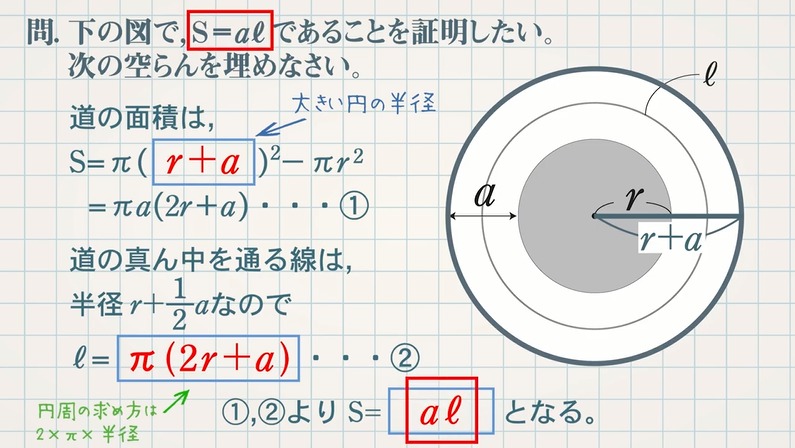



S Aℓの証明 式の計算の利用 図形編 教遊者



1




中2 数学ー図形の性質と証明ー 中学生 数学のノート Clear




平行四辺形の定義と性質 証明問題の解き方 数学fun




中学数学 図形の合同 図形の性質




世界一わかりやすい数学問題集中2 5章 図形の性質と証明



Studydoctor図形の性質と相似の証明 中3数学 Studydoctor




図形の性質と証明の練習問題1 数学の要点まとめ 練習問題一覧



Http Www Pref Chiba Lg Jp Kyouiku Shidou Gakuryoku Yaruki Suugaku Documents M14 Pdf




図形の性質 の問題のわからないを5分で解決 映像授業のtry It トライイット




内心とは 三角形の内心の求め方や比の使い方 性質の証明 位置ベクトルをわかりやすく解説 遊ぶ数学




5章 図形の性質と証明 愛知県公立高校入試 数学 単元別過去問 問題プリントと解答 解説
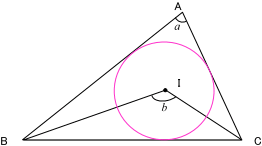



図形の証明の考え方 数学 苦手解決q A 進研ゼミ高校講座




正三角形 正方形を利用した合同の証明 ドリるーむ




図形に関する性質の証明 身勝手な主張




垂心の証明 座標を用いた図形の性質の証明 数学ii By ふぇるまー マナペディア




図形の性質と証明 数スタ



Http Toro J Saitama City Ed Jp Kadai 3nenn Kyouka 2suugaku Seisitutosyoumei Monndai Pdf




図形に関する性質の証明 身勝手な主張




中2 中2 図形の性質と証明 中学生 数学のノート Clear



数学a 平面図形 円の性質 円の接線




世界一わかりやすい数学問題集中2 5章 図形の性質と証明




中3数学 道路の面積を求める問題 例題編 映像授業のtry It トライイット
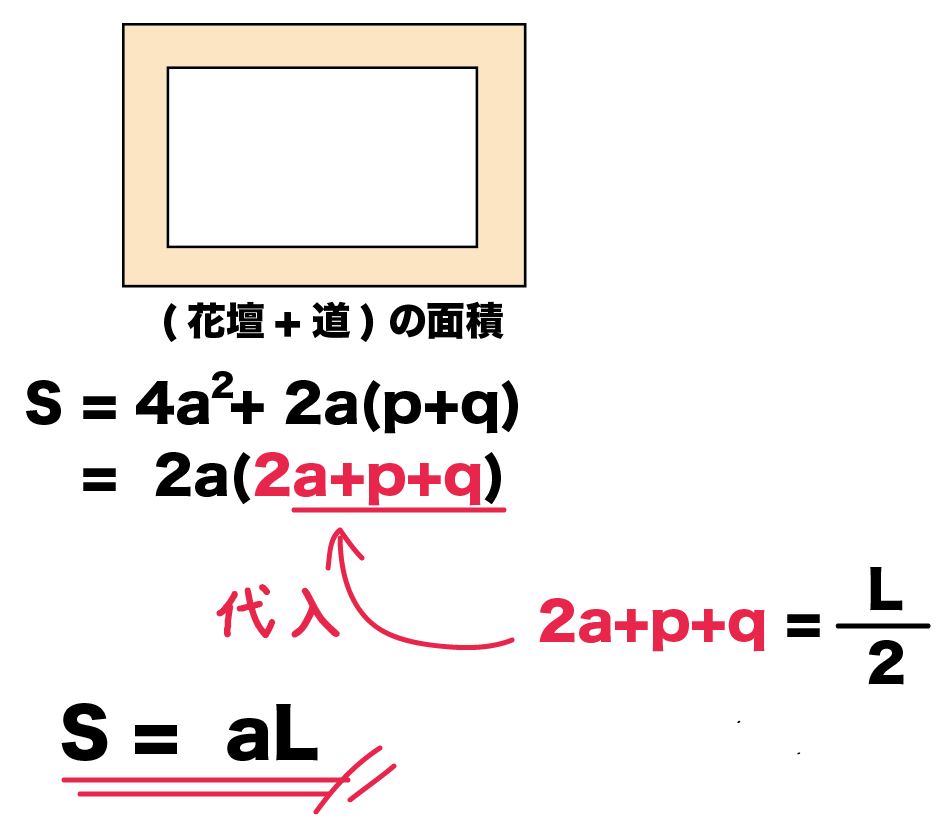



式の計算の利用 図形の証明問題の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく
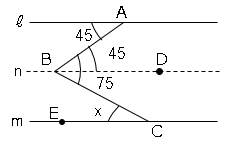



図形の性質と証明の練習問題1 数学の要点まとめ 練習問題一覧




中2数学 図形の調べ方 と 図形の性質と証明 の基礎を解説 札幌市 西区 琴似 発寒 塾 学習塾 個別指導塾 マナビバ
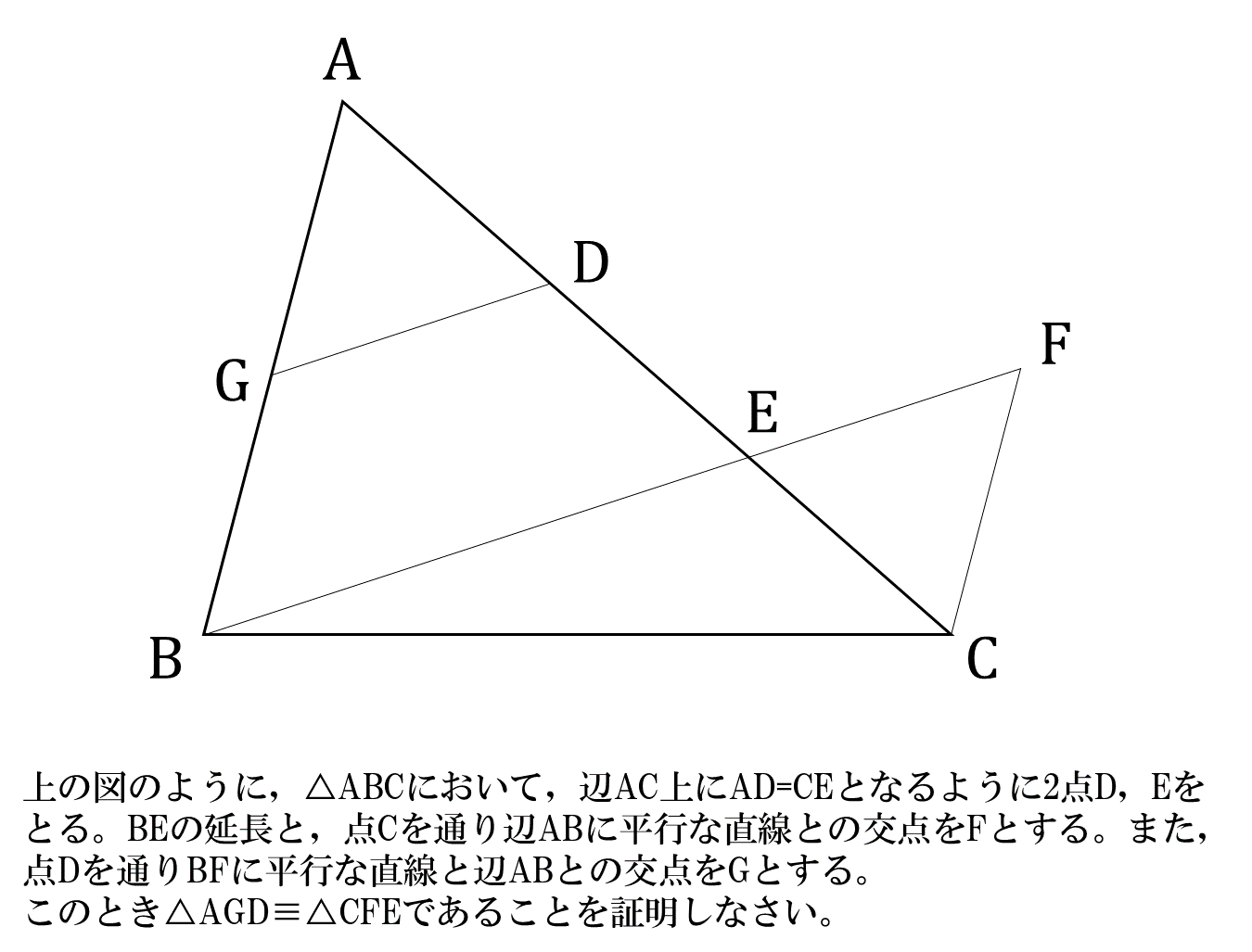



数学 中学証明問題を解く4つのポイント




中学2年生 数学 三角形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




世界一わかりやすい数学問題集中2 5章 図形の性質と証明




世界一わかりやすい数学問題集中2 5章 図形の性質と証明




中学校数学 証明のコツ 入試問題 基本図形



角の二等分線の性質と二等分線の長さ 思考力を鍛える数学




高校数学 複素数による図形の性質の証明 受験の月



Www Pref Chiba Lg Jp Kyouiku Shidou Gakuryoku Zissenmoderu Documents C 053 Pdf




図形の性質と証明の練習問題1 数学の要点まとめ 練習問題一覧




高校数学a 三角形の内角 外角の二等分線と辺の比の関係とその証明 受験の月



0 件のコメント:
コメントを投稿