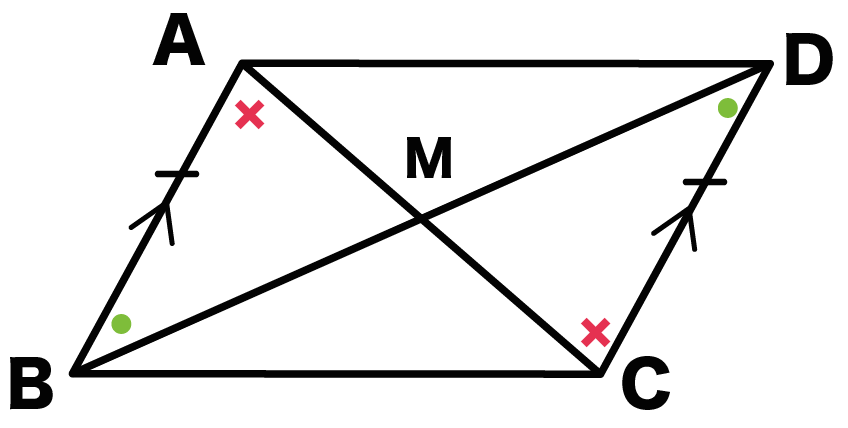
ユークリッド原論をどう読むか(3) 頁末 前 次 目次 ユークリッド原論 第1巻 命題1ー34(平行四辺形の対辺・対角・対角線) 平行四辺形・対角線 (平行四辺形と長斜方形とは同義) (平行四辺形の対角線は互いに他を2等分)長方形・ひし形は平行四辺形の一種なので、平行四辺形の対角線の性質を持っています。 さらに、『すべての角が直角』の長方形と『すべての辺の長さが等しい』ひし形ですが、これらの定義とは対象的に対角線については長方形が 『対角線の長さが等しい』 、ひし形が 『対角線が直交する上のまとめに示したように「平行四辺形」の定義は「2組の向かい合う辺がそれぞれ平行である四角形」すなわち「 ad//bc , ab//dc 」が成り立つ四角形なので,仮定や結論が「平行四辺形」になっているときは「 ad//bc , ab//dc 」に置き換えるとよい この頁では平行線の性質について,証明の進め方

平行四辺形の定義から性質と条件をわかりやすく証明 特に対角線の性質を押さえよう 遊ぶ数学
平行四辺形の定義 証明
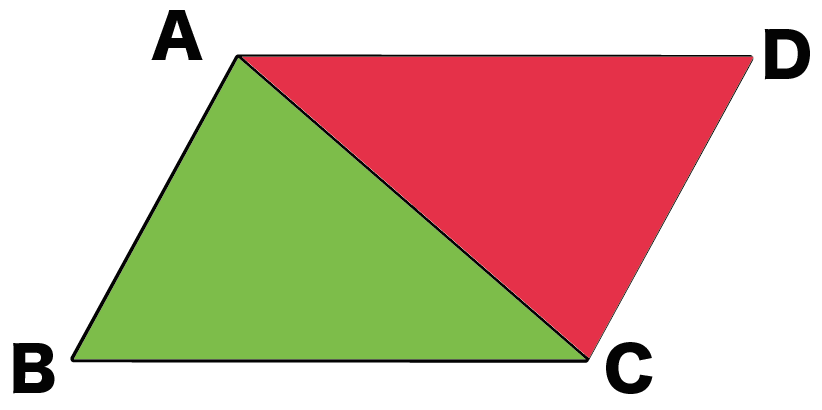
平行四辺形の定義 証明-証明 それぞれの中点で交わるので四角形abcdは平行四辺形になる。 abcと dcbで 平行四辺形abcdの性質より ab=dc 1 bc=cb(共通) 2 仮定(対角線の長さが等しい)より ac=db 3 1,2,3より3辺がそれぞれ等しいので・ 平行四辺形の定義や性質を使って、図形の性質を証明したり、辺の長さや角の 大きさを求めたりすることができる。 ・ 平行四辺形の性質を使って、課題を解くことができる。



平行四辺形になるための証明1
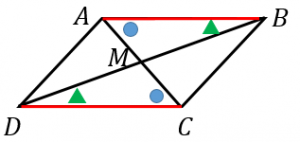
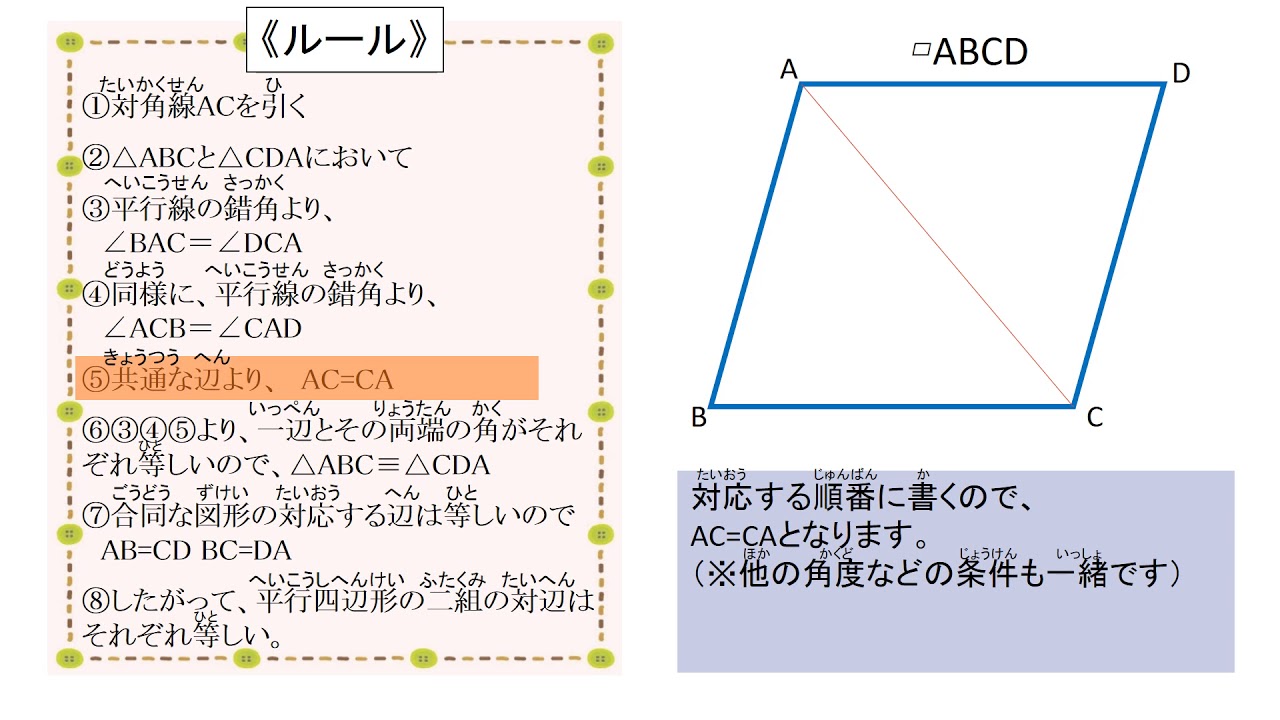
数学・算数 平行四辺形の証明 平行四辺形の証明において、 (1)対辺は等しい。 (2)対角は等しい。 (3)対角線は互いに他を二等分する。 という三つの証明を各々どう証明すればよいのかと聞かれて 質問No⑤ $\textcolor{blue}{1}$ 組の対辺が平行でその長さが等しい →定義・性質では出てこないけど、「平行四辺形であること」の証明ではよく使われます。 ①は平行四辺形の 定義 ②、③、④は平行四辺形のそれでは、これで証明の大まかな道筋が見えたので、ここから証明を書いていきます。 <証明> EOAと FOCにおいて 平行四辺形の対角線はそれぞれの中点で交わるので OA=OC ① 対頂角は等しいので ∠EOA=∠FOC ② 平行四辺形の対辺は平行なので、ED//BF
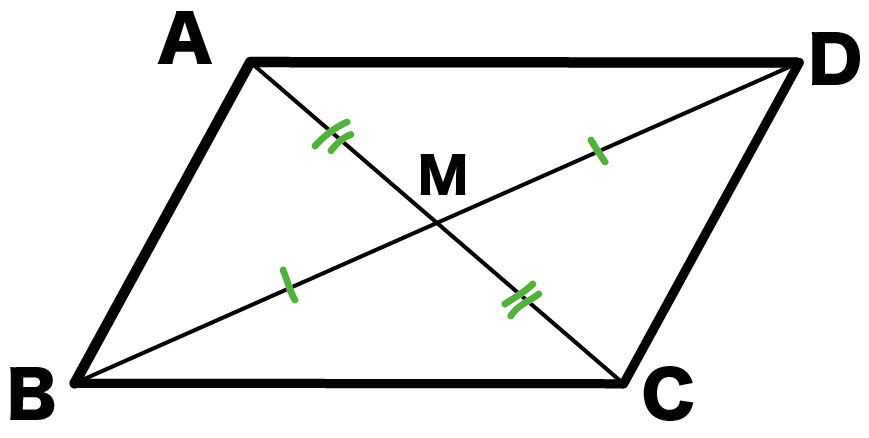
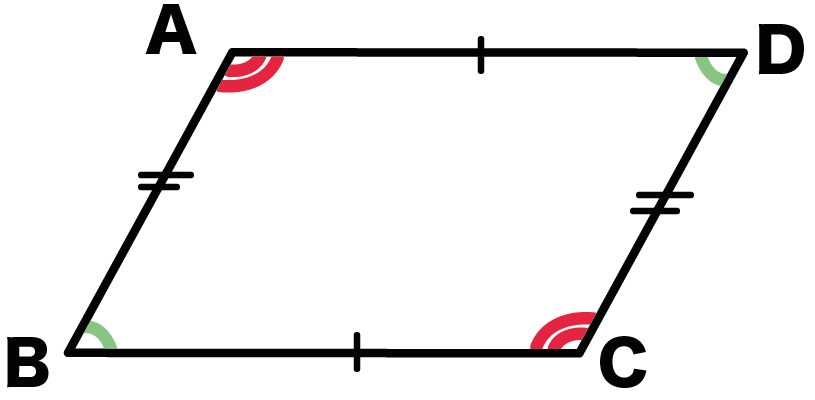
平行四辺形 平行四辺形の定義 2組の対辺がそれぞれ平行な四角形 平行四辺形の定義からつぎの性質を導くことができる 2組の対辺はそれぞれ等しい。 >>証明 2組の対角はそれぞれ等しい。 >>証明 対角線はそれぞれの中点で交わる。2組の向かい合う辺(対辺)がそれぞれ等しい四角形は、平行四辺形である。 ③ 2組の向かい合う角(対角)がそれぞれ等しい四角形は、平行四辺形である。 ④ 対角線が、それぞれの中点で交わる四角形は、平行四辺形である。 (3) ① (定義だから) 2平行四辺形とひし形の違いってなに??←今回の記事 平行四辺形の角度、辺の長さを求める問題を解説! 平行四辺形の中から面積の等しい三角形を見つける問題を徹底解説! 等積変形三角形の面積問題と作図のやり方は?証明問題も紹介!
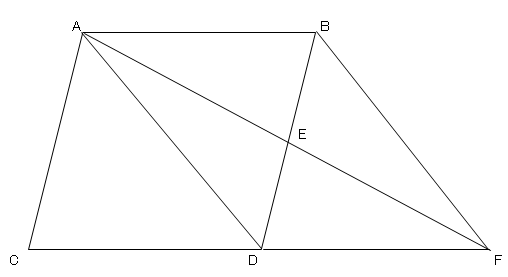
平行四辺形の練習問題(平行四辺形になることの証明) 平行四辺形abcdの辺ab,cd,da上に,それぞれ,点e,f,g,hを,ae=cg,bf=dhとなるようにとります。このとき,四角形efghは,どんな四角形になりますか。証明し答えなさい。 平行四辺形解答2 aehと cgf において 仮定より7.平行四辺形の証明問題 ①2組の向かいあう辺が、それぞれ平行な四角形(とき) <定義> (条件) ②2組の向かいあう辺が、それぞれ等しい(とき) <性質>(条件)Z証明 { aomと conにおいて 平行線の錯角は等しいからad//bcより ∠mao=∠nco・・・① 平行四辺形の対角線はそれぞれの中点で交わるから ao=co・・・② 対頂角は等しいから ∠aom=∠con・・・③ ①~③より1組の辺とその両端の角がそれぞれ等しいから abd≡ con



平行四辺形の証明 2 ネット塾




中2数学 平行四辺形の3大重要ポイント 映像授業のtry It トライイット
平行四辺形の定義となる。 (以下、定義1ー22の補足2(平行四辺形) という。) 命題1ー34は平行四辺形が長斜方形であることを論証している。 矩形のことを方形ともいう。 (以下、定義1ー22の補足3(方形) という。) <平行線> 定義1ー23(平行(線〔証明〕ひし形abcdの対角線ac,bdの交点をoとする。 aboと ( )において ひし形の定義から ( )=( ) ・・・1 ひし形は平行四辺形だから 対角線はそれぞれの中点で交わるから ( )=( ) ・・・2 また定義は 「こういう四角形を平行四辺形としよう」 と決めたことなので、これを証明することはできません。 「なぜ平行四辺形の向かい合う2組の辺は平行なのか?




中2数学 平行四辺形の証明の定期テスト予想問題 Pikuu



Tossランド 平行四辺形の性質
定義できる 特に, 平面のx 軸, y 軸の方向は右手系をなす 右手を左手に入れ換えて左手 系が定義される a b c 2 面積と体積 21 平行四辺形の面積 n 次元ベクトルa,b の作る平行四辺形(右下図) の面積をS とすれば, a,b のなす角をθ (0 ď θ ď π) として,これが平行四辺形の定義です。 平行四辺形というのは、定義としては、向かいあう辺が平行であることしか決めていません。 しかし、そこから言えることがいくつもあります。 それが定理です。 定理というのは、証明できる事柄のうち、重要なこと平行四辺形の定義から性質と条件をわかりやすく証明 特に対角線の性質 平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを 中2数学 基本解説 問題 233 平行四辺形3 長方形とひし形 プリント 平行四辺形abcdの対角線を



平行四辺形になる条件



中2数学 平行四辺形の性質がわかる3つの証明 Qikeru 学びを楽しくわかりやすく
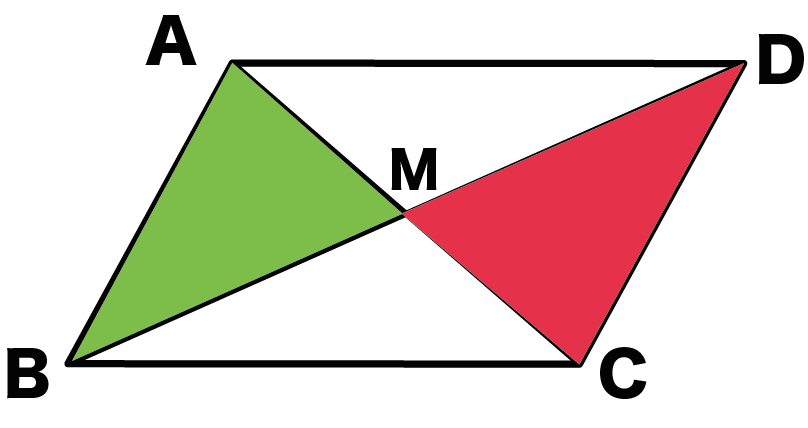
平行四辺形 今回は,平行四辺形について学びます.内容はそれほど難しくは ありません. 内容より,数学における議論の進め方,すなわちすでに証明した 事実だけを用いて,次の命題を証明することに注目してください.また,平行四辺形の向かい合う辺は等しいので, x =CF 7 -4 3cm, y AG 10 6 4cm 問題(後期期末)平行四辺形の性質3 a b c d 平行四辺形の定義(ab//cd, ad//cb)から、「対角線はそれぞれの中点で交わる」を証明する。



中点連結定理を使った平行四辺形であることの証明 教遊者




平行四辺形の性質 長さ 角度の問題 無料で使える中学学習プリント
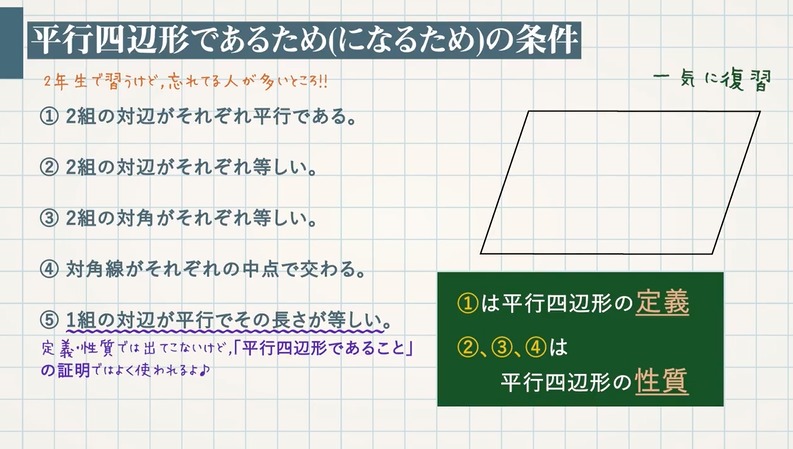
「定義」 :こういうものを平行四辺形と呼ぼう! 「性質」 :平行四辺形と呼ばれるものには 共通してこんなことが言えるね! 「定理」 :性質の中で特に大切なこと! だから証明はいらないよ! こんな感じです。 例えば、コーラ。 定義:黒くてシュワ同様にして,四角形GDFI も平行四辺形で, b =∠DGI=180°- a =180°-110°=70°平行四辺形の定義 ①定義 2組の対辺がそれぞれ平行である。 ②定理 2組の対辺がそれぞれ等しい。 ③定理 2組の対角がそれぞれ等しい。



平行四辺形の証明 1 ネット塾



平行四辺形になるための証明1
解説 平行四辺形の定義から,正しく証明がなされ,結論を導き出していることを確 認した上で,証明は命題が例外なしに成り立つことを明らかにする方法であるの で,ウになる。こんにちは、ウチダです。 今日は、中学 $2$ 年生の内容である 「平行四辺形になるための $5$ つの条件」 について、平行四辺形の定義から性質を証明し、そのあとで性質と条件が具体的にどう違うのかを詳しく見ていきましょう。 平行四辺形の定義とは まず、「平行四辺形とは何か」口で説明「平行四辺形」は 「向かい合っている辺の長さ」 が等しく、 「向かい合っている角の大きさ」 も等しい四角形だよね。 「長方形」 は、平行四辺形の 角度が進化 するよ。すべての角の大きさが等しく 、つまり 90°




中2数学 平行四辺形の3大重要ポイント 映像授業のtry It トライイット



中2数学 平行四辺形の性質と証明の要点まとめノート 中学生勉強サイトあかね先生
平行四辺形になる条件 四角形は、次の性質のどれかをもつと、平行四辺形である。 1 2組の向かいあう辺が、それぞれ平行である。(定義) 2 2組の向かいあう辺が、それぞれ等しい。(証明) 3 2組の向かいあう角が、それぞれ等しい。(証明)平行四辺形の定義 2組の対辺がそれぞれ 平行な四角形 性質1 2組の対辺は それぞれ等しい 性質2 2組の対角は それぞれ等しい 性質3 対角線はそれぞれの 中点で交わる。4つの角がすべて等しい四角形 が「長方形の定義」っておぼえておこう。 長方形は平行四辺形の仲間なの?? 1つだけおさえておきたいことがある。 それは、 長方形は平行四辺形の1種 ってことさ。 つまり、 長方形は平行四辺形である といえちゃうんだ。




中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット




中2数学 平行四辺形の性質の利用 練習編 映像授業のtry It トライイット
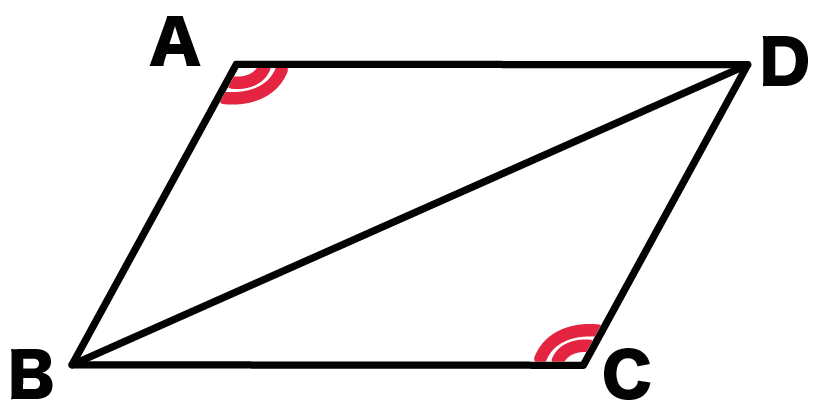
特別な三角形・四角形の定義とその証明 幾何 宮部 宏成 高校入試でも定期テストでも頻出の 特別な図形その定義と証明をわかりやすく解説します! Contents 1 二等辺三角形 11 二等辺三角形 12 2つの角が等しい三角形 13 正三角形 14 定理の逆台形の定義 1組の対辺が平行である四角形 平行四辺形の定義 2組の対辺がそれぞれ平行な四角形 長方形の定義 4つの角がすべて等しい四角形(4つの角がみな直角である) ひし形の定義 4つの辺がすべて等しい四角形 正方形の定義2年生 5 図形の性質と証明 知識・技能の習得を図る問題 年 組 号 氏名 全国学力・学習状況調査 A問題 ② 2 下のように「平行四辺形の2組の向かい合う辺はそれぞれ等しい」ことを証明しました。
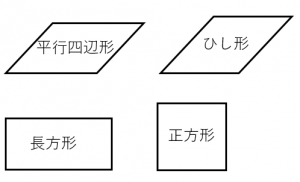



平行四辺形 ひし形 長方形 正方形の違い 具体例で学ぶ数学



平行四辺形の性質を使った証明 平行四辺形になることの証明 チーム エン
平行四辺形の定義は、「\(\boldsymbol{2}\) 組の向かい合う辺が平行な四角形を平行四辺形という 」になります。また、平行四辺形になるためには、定義を含めて \(\boldsymbol{5}\) つの条件 があります。




平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ




中2 数学 中2 証明 中学生 数学のノート Clear
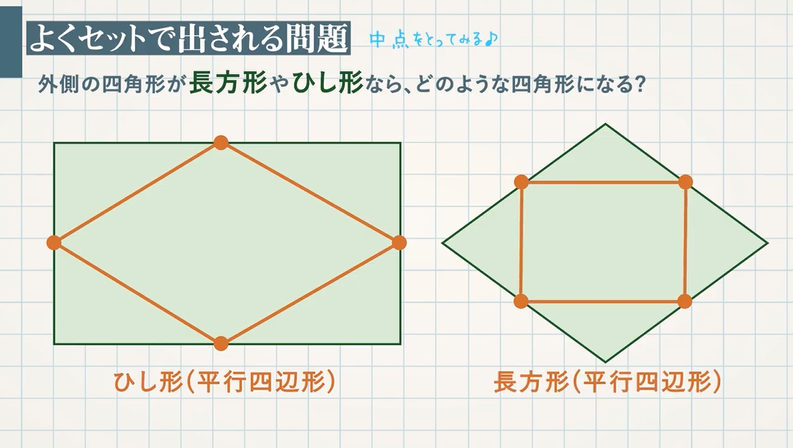



中点連結定理を使った平行四辺形であることの証明 教遊者



中2数学 平行四辺形の性質がわかる3つの証明 Qikeru 学びを楽しくわかりやすく



Katekyo学院山形 中学生 証明問題 21 1 27




平行四辺形の定義と性質 証明問題の解き方 数学fun



中2数学 平行四辺形の性質がわかる3つの証明 Qikeru 学びを楽しくわかりやすく




等脚台形の定義と性質 中学校数学の範囲内で考える 身勝手な主張




平行四辺形の定義から性質と条件をわかりやすく証明 特に対角線の性質を押さえよう 遊ぶ数学




1 T Descubre Como Resolverlo En Qanda




三角形と四角形 平行四辺形であることの証明の仕方 中学数学 定期テスト対策サイト



中2数学 平行四辺形の性質がわかる3つの証明 Qikeru 学びを楽しくわかりやすく



1




中学校数学 証明のコツ 年01月
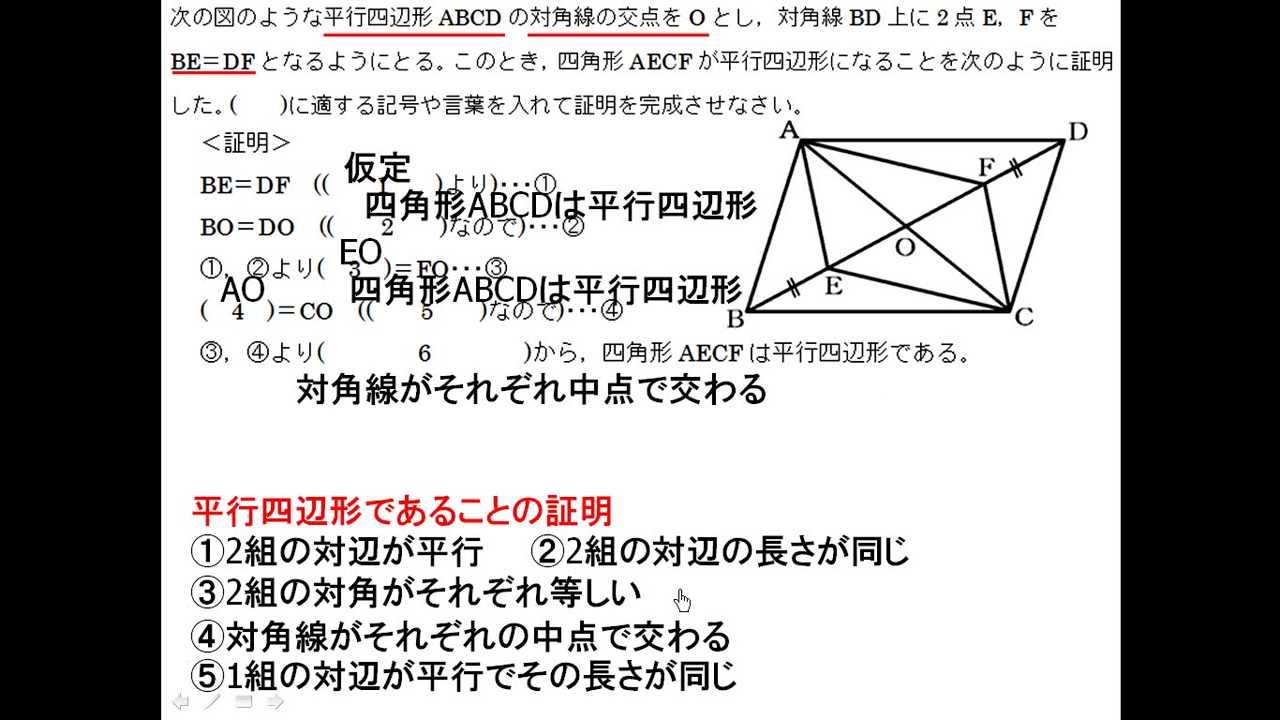



中2 数学 5 3 平行四辺形の証明 Youtube
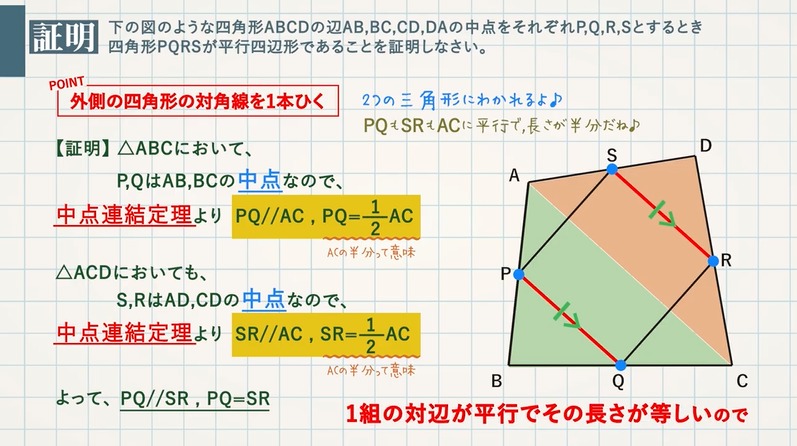



中点連結定理を使った平行四辺形であることの証明 教遊者



数学の証明の問題です 平行四辺形abcdの外側に 辺ab をそれ Yahoo 知恵袋



中2数学 平行四辺形の証明のポイントと練習問題 Examee
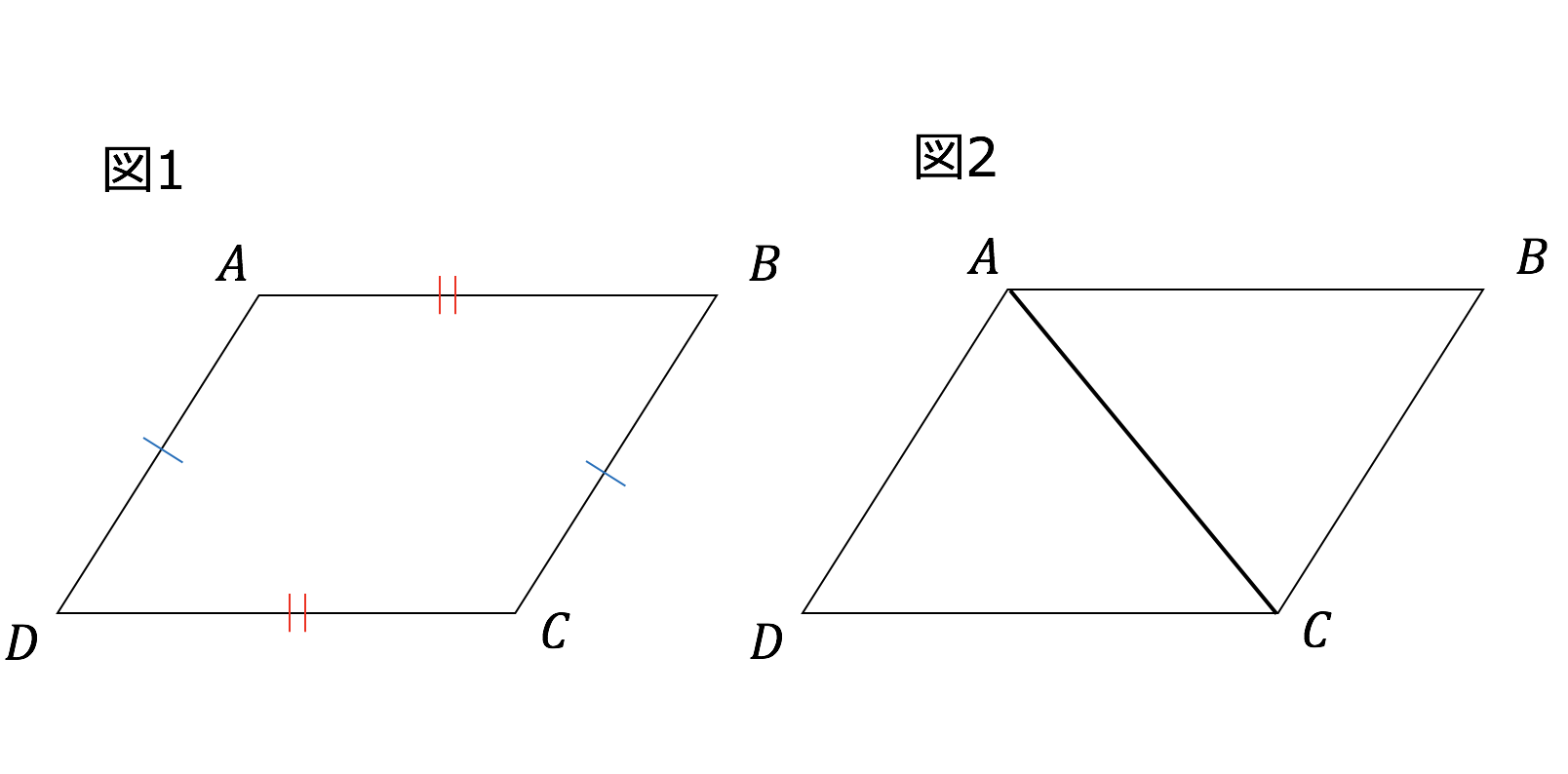



3分で分かる 平行四辺形とは 定義や性質 成立条件をわかりやすく 合格サプリ




中2数学 平行四辺形の3大重要ポイント 映像授業のtry It トライイット




これ 問題の中に1つも平行ってワードがないのに どうして中点連結定理になるのか そし Clear




平行四辺形と証明 Youtube




中2の数学の問題です 平行四辺形になるための条件の部分で 対角線がそれぞれ中点で交わ Clear




中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット



平行四辺形の3つの性質とその証明 具体例で学ぶ数学




無料 中2数学 基本解説 解答プリント 230 平行四辺形1 性質




中学校数学 証明のコツ 平行四辺形と錯角 同位角の相互関係を理解する過程で 証明する力を確実に伸ばすことができる自学自習教材



Math 平行四辺形 平行四辺形になることの証明 働きアリ The 2nd




中学校数学 証明のコツ 平行四辺形と錯角 同位角の相互関係を理解する過程で 証明する力を確実に伸ばすことができる自学自習教材




平行四辺形を使った証明 Youtube



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典




平行四辺形の性質の証明 中学数学教材研究ノート




平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ
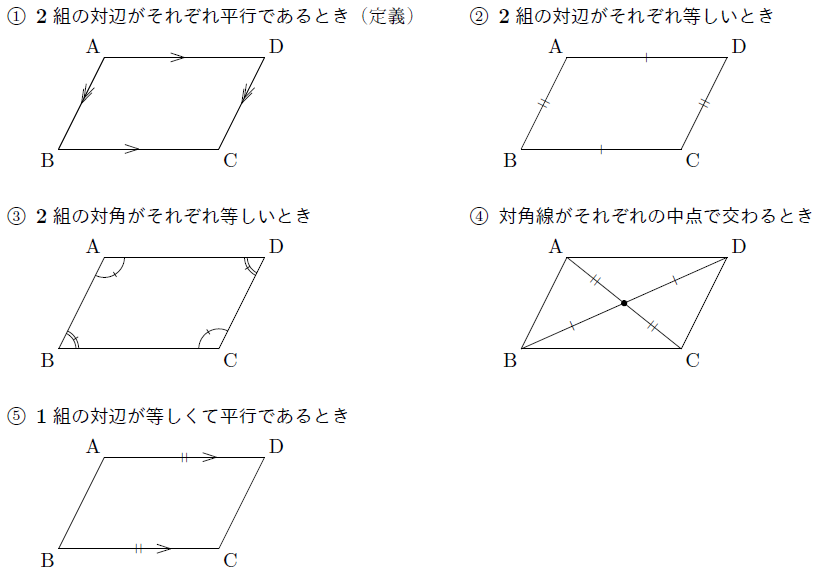



平行四辺形になるための条件 まなびの学園




平行四辺形 中学数学で遊ぶ 身勝手な主張




平行四辺形になるための条件 Youtube
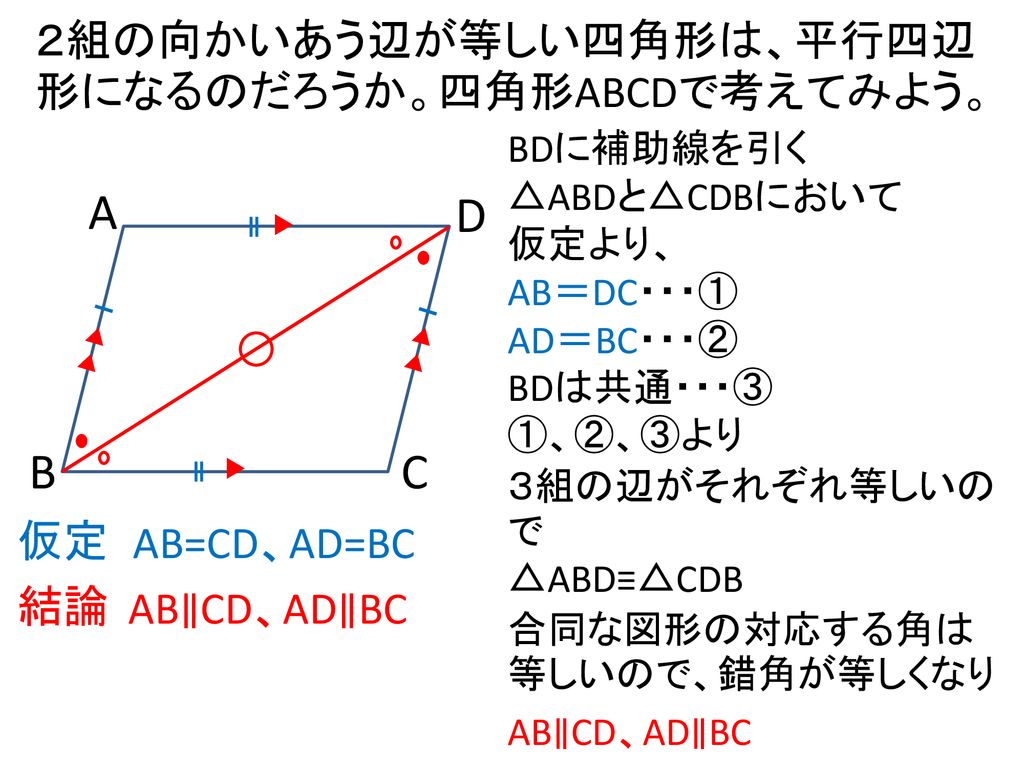



ねらい 平行四辺形の性質の逆を証明し 平行四辺形になるための条件を導くことができる Ppt Download



1




Math 平行四辺形 平行四辺形になることの証明 働きアリ
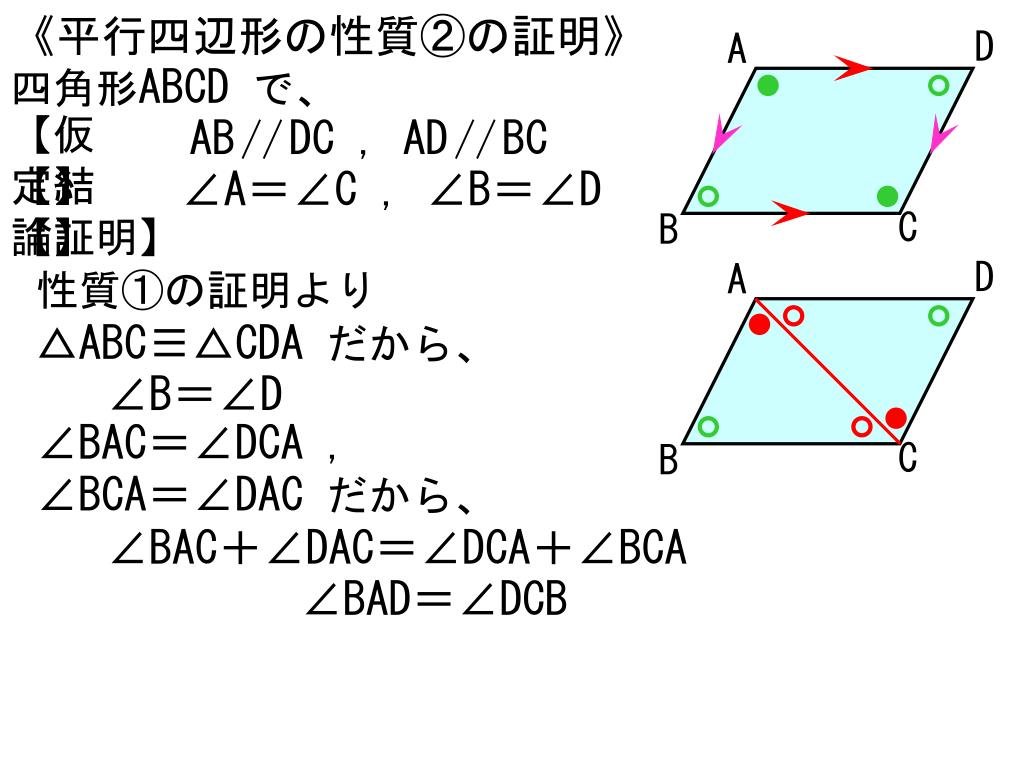



Ppt 5 図形と合同 Powerpoint Presentation Free Download Id



中2数学 平行四辺形の性質がわかる3つの証明 Qikeru 学びを楽しくわかりやすく




中点連結定理とは 逆の証明や平行四辺形の問題もわかりやすく解説 遊ぶ数学




中2数学 平行四辺形の証明 練習編 映像授業のtry It トライイット




ねらい 平行四辺形の定義と性質を理解し 定義から導かれた性質を 三角形の合同条件などを使って証明することができる Ppt Download



合同な三角形 平行四辺形で証明 苦手な数学を簡単に




bc Ab Ac D E De De Ef Descubre Como Resolverlo En Qanda



高校入試 英語 数学 学習 三角形と四角形 平行四辺形




平行四辺形の証明と角度を求める問題の解き方 現役塾講師のわかりやすい中学数学の解き方



平行四辺形になる条件




高校数学b ベクトルの成分表示と平行四辺形 受験の月




平行四辺形の定理や定義 平行四辺形の覚えておきたい性質は4つ 中学や高校の数学の計算問題



1




平行四辺形 現役塾講師のわかりやすい中学数学の解き方



中学数学 証明 平行四辺形の性質の利用 中学数学の無料オンライン学習サイトchu Su




中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット




定義と定理 12月 年 光が丘中学校 ブログ 光が丘中学校




中学数学 特別な平行四辺形について Clear



平行四辺形の性質 中学2年 数学クラブ



平行四辺形の3つの性質とその証明 具体例で学ぶ数学



3
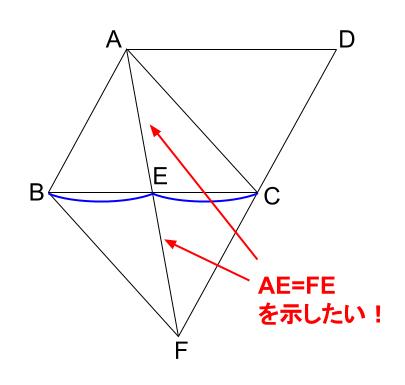



中学数学 平行四辺形になることの証明 その2 中学数学の無料オンライン学習サイトchu Su




中学校数学 証明のコツ 年01月




平行四辺形の面積の公式 なぜ 底辺 高さ で求められるのか 数学fun
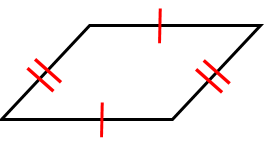



平行四辺形の3つの性質とその証明 具体例で学ぶ数学




平行四辺形であることを証明する 苦手な数学を簡単に
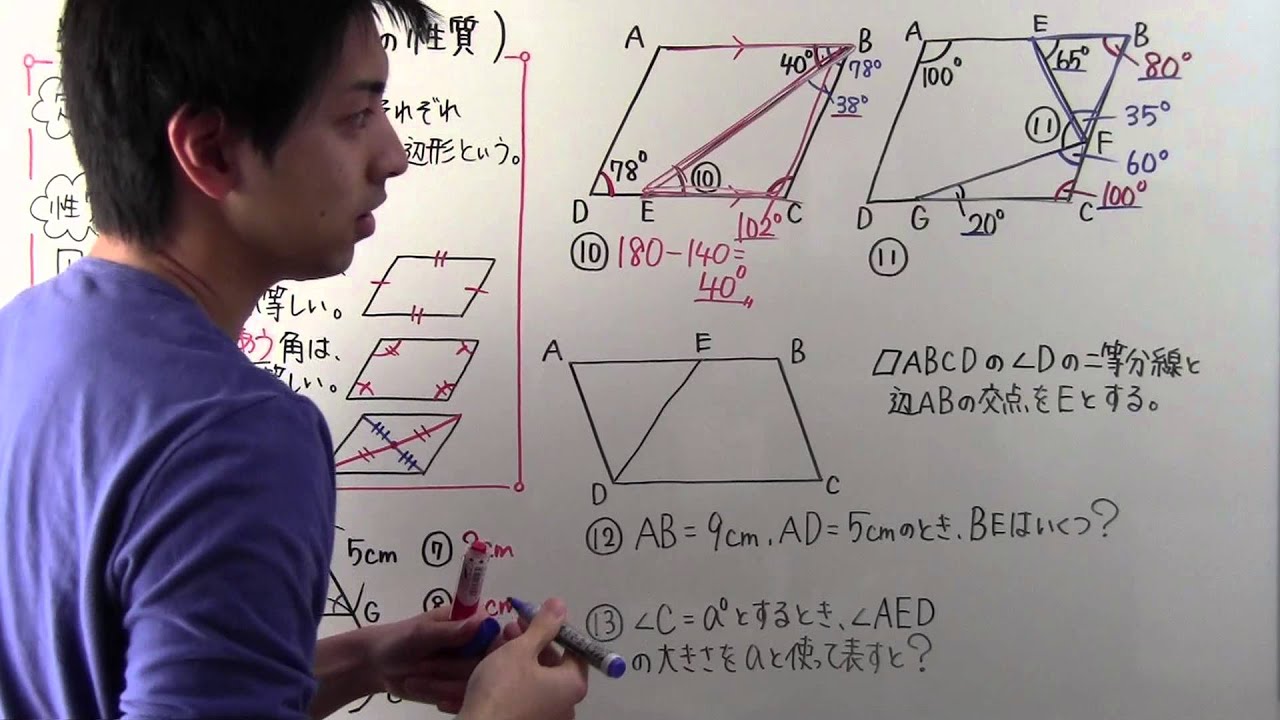



数学 中2 73 平行四辺形の性質 Youtube




中2 授業ノート 平行四辺形の性質 中学生 数学のノート Clear




高校入試と 平行四辺形の定義と定理について 中学生 受験対応 英語 数学 学習講座




画像をダウンロード 平行 四辺 形 特徴 ニスヌーピー 壁紙
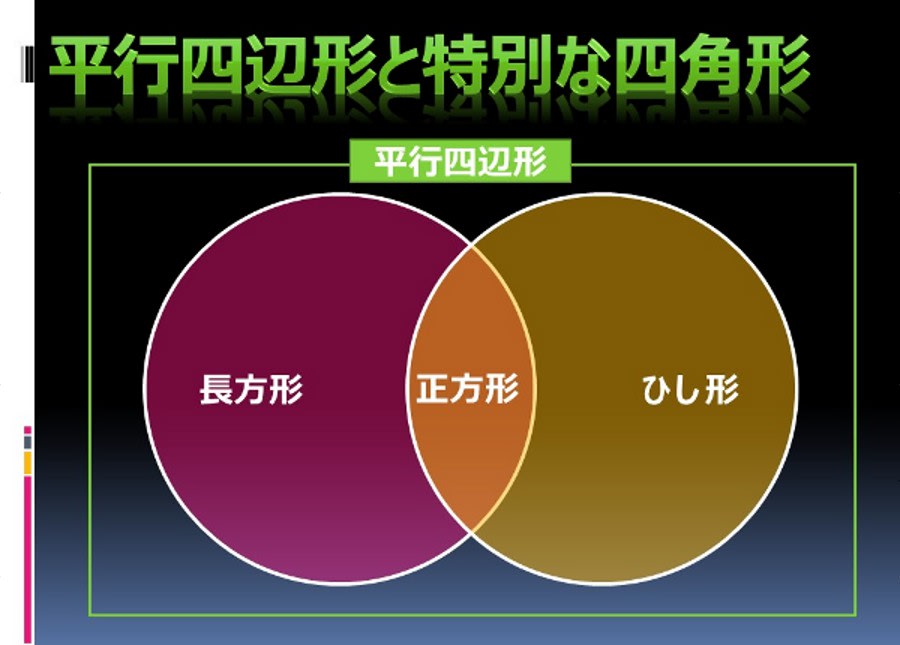



高校入試と 平行四辺形の定義と定理について 中学生 受験対応 英語 数学 学習講座




3分で分かる 平行四辺形とは 定義や性質 成立条件をわかりやすく 合格サプリ




中2 中2数学 平行四辺形の証明 授業ノート 中学生 数学のノート Clear
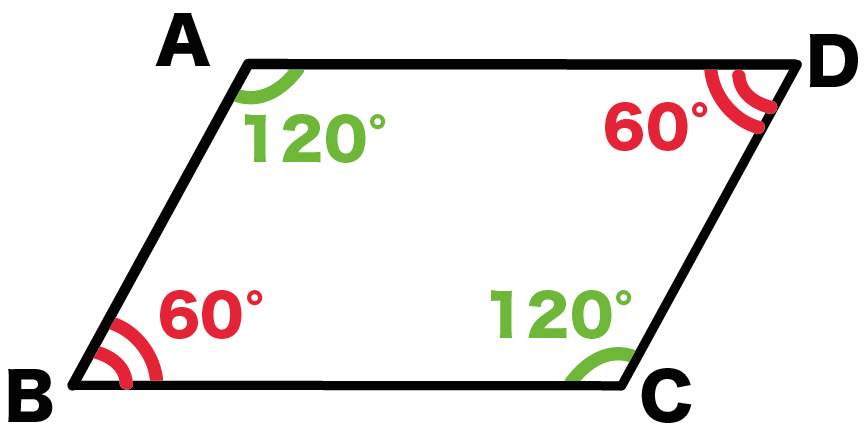



中2数学 平行四辺形の3つの性質 Qikeru 学びを楽しくわかりやすく



平行四辺形になる条件




平行四辺形の定義 定理 性質 と証明問題 中学数学の図形 リョースケ大学
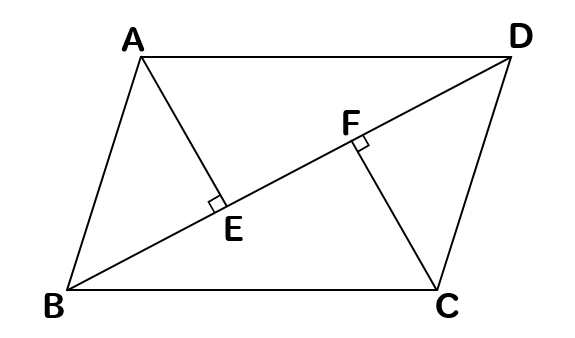



中学数学 平行四辺形の証明問題を徹底解説 数スタ




数学 中2 74 平行四辺形になる条件 Youtube
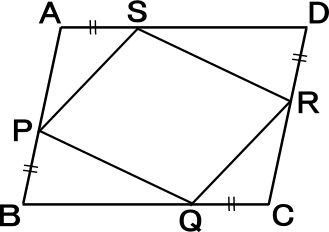



中学2年数学練習問題 平行四辺形になる条件と証明方法 図形と合同



平面図形の基礎




特別な平行四辺形 画質上 Youtube




平行四辺形になることの証明 Youtube




台形と平行四辺形を平行な辺の組の数で分類することは 原理的に不可能である 小学校4年生の算数 身勝手な主張
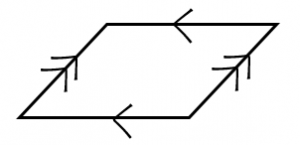



平行四辺形の3つの性質とその証明 具体例で学ぶ数学



中2 平行四辺形の性質の証明1 対辺 日本語版 Youtube



中2数学 平行四辺形の性質がわかる3つの証明 Qikeru 学びを楽しくわかりやすく




平行四辺形の対角線は中点で交わる ことの説明 おかわりドリル




平行四辺形になる条件 小学生 中学生の勉強




中2数学 平行四辺形 長方形 ひし形 正方形の違い 映像授業のtry It トライイット



0 件のコメント:
コメントを投稿